Teori Peluang   »   Peubah Acak   ›  Moment Generating Function

Peubah Acak

Moment Generating Function

Fungsi pembangkit momen (moment generating function) merupakan fungsi yang dapat menghasilkan momen-momen. Momen-momen yang dihasilkan ini bisa digunakan untuk mencari nilai harapan, nilai rataan dan varians dari suatu peubah acak.

---

Fungsi pembangkit momen (moment generating function/MGF) merupakan fungsi yang dapat menghasilkan momen-momen. Momen-momen yang dihasilkan ini bisa digunakan untuk mencari nilai harapan, nilai rataan dan varians dari suatu peubah acak. Tidak hanya itu, fungsi pembangkit momen juga bisa digunakan untuk mencari distribusi dari suatu peubah acak yang baru.

Dari definisi di atas kita tahu bahwa \(M_X (t)=E(e^{tx})\). Jika kita uraikan persamaan ini dengan menggunakan perluasan Deret MacLaurin, maka akan diperoleh:

Kemudian, jika kita melakukan diferensiasi atau turunan \(M_X (t)\) yang telah diperluas dengan deret MacLaurin tersebut terhadap \(t\), maka akan diperoleh hasil sebagai berikut:

Jika kita menetapkan nilai \(t=0\) pada hasil turunan tersebut, maka kita akan peroleh hasil berikut ini:

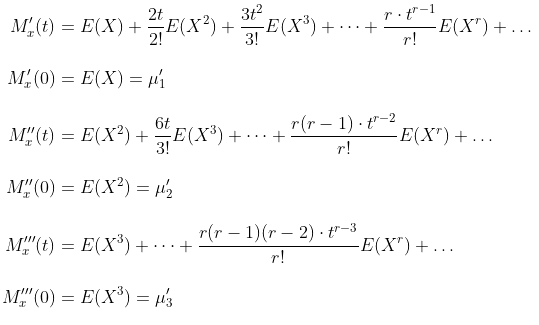
Demikian seterusnya, jika \(M_X (t)\) diturunkan terhadap \(t\) sebanyak \(r\) kali, dan kemudian menetapkan nilai \(t\) sama dengan nol \((t=0)\) maka akan diperoleh:

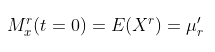
Dengan demikian dapat kita simpulkan bahwa momen ke-\(r\) yang dinotasikan dengan \(u_r\) bisa diperoleh melalui fungsi pembangkit momen. Dengan kata lain, fungsi pembangkit momen merupakan sebuah fungsi yang dapat menghasilkan momen-momen sehingga tidak heran jika nama yang diberikan kepadanya adalah fungsi pembangkit momen.

Seperti dinyatakan di awal artikel ini, fungsi pembangkit momen bisa digunakan untuk mencari nilai rataan atau nilai harapan dan varians dari suatu variabel acak. Nilai harapan peubah acak ini dapat diperoleh dari turunan pertama fungsi MGF terhadap \(t\) dan menetapkan nilai \(t = 0\) pada hasil turunan tersebut. Dengan demikian,

Selanjutnya, untuk mencari varians, kita perlu mencari momen kedua dari fungsi MGF terlebih dahulu. Hal ini dapat dilakukan dengan melakukan turunan sebanyak dua kali terhadap \(M_X (t)\) dan kemudian menetapkan nilai \(t = 0\). Berikut adalah hasil yang diperoleh:

Dengan demikian, varians dari suatu peubah acak adalah:

Teorema-teorema Terkait MGF

Bukti:

\begin{aligned} M_{X+a} (t) &= E \left[ e^{t(X+a)} \right] \\[8pt] &= e^{at} \ E(e^{tX} ) \\[8pt] &= e^{at} \ M_X(t) \end{aligned}

Bukti:

\begin{aligned} M_{aX} (t) &= E \left[ e^{t(aX)} \right] \\[8pt] &= E(e^{(at)X} ) \\[8pt] &= M_X(at) \end{aligned}

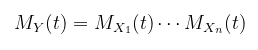
Bukti:

Karena

maka,