www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Peubah Acak › Nilai Harapan suatu Peubah Acak
Peubah Acak
Nilai Harapan suatu Peubah Acak
Nilai harapan peubah acak diskret diperoleh dengan mengalikan tiap nilai dari peubah acak dengan peluang padanannya dan kemudian menjumlahkan hasilnya.
Rataan atau nilai harapan suatu peubah acak diskret dapat dihitung dengan mengalikan tiap nilai \(x_1,x_2,..,x_n\) dari peubah acak X dengan peluang padanannya \(f(x_1),f(x_2),…,f(x_n)\) dan kemudian jumlahkan hasilnya.
Jika peubah acaknya adalah kontinu, cara penghitungan nilai harapan masih sama dengan yang peubah acak diskret tetapi kita perlu mengganti penjumlahan dengan integral.
DEFINISI:
Misalkan X suatu peubah acak dengan distribusi peluang \(f(x)\). Nilai harapan atau rataan X didefinisikan sebagai berikut:

CONTOH 1: Kasus Diskrit
Carilah nilai harapan banyaknya kimiawan dalam panitia 3 orang yang dipilih secara acak dari 4 kimiawan dan 3 biolog.
Penyelesaian:
Misalkan peubah acak \(X\) menyatakan banyaknya kimiawan dalam panitia, maka distribusi peluang \(X\) adalah
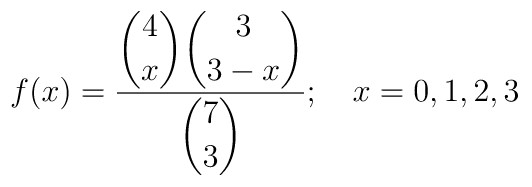
Selanjutnya kita cari nilai peluang ketika x = 0, 1, 2, dan 3. Adapun hasil perhitungannya yaitu:

Dengan demikian, kita peroleh hasil berikut:

Jadi, bila suatu panitia beranggota 3 orang dipilih secara acak dari 4 kimiawan dan 3 biolog, maka rata-ratanya akan beranggota 1,7 kimiawan.
CONTOH 2: Kasus Diskrit
Dalam suatu permainan seseorang mendapat Rp5 bila dalam lantunan 3 uang logam muncul semua muka atau semua belakang, dan membayar Rp3 bila muncul muka satu atau dua. Berapakah harapan kemenangannya?
Penyelesaian:
Misalkan \(T\) menyatakan ruang sampel untuk semua kemungkinan hasil bila 3 uang logam dilantunkan sekaligus, atau sama saja dengan bila 1 uang logam dilantunkan 3 kali, ialah
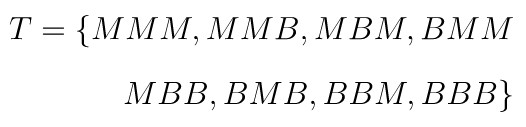
Perhatikan bahwa tiap titik sampel berpeluang sama dan masing-masing terjadi dengan peluang 1/8.
Sekarang misalkan peubah acak \(Y\) menyatakan besarnya kemenangan; maka kemungkinan nilai \(Y\) ialah Rp5 bila kejadian yang muncul adalah \(E_1=\{MMM,BBB\}\) dan bernilai -Rp3 bila kejadian yang muncul adalah

Karena \(E_1\) dan \(E_2\) terjadi masing-masing dengan peluang \(¼\) dan \(¾\) , maka
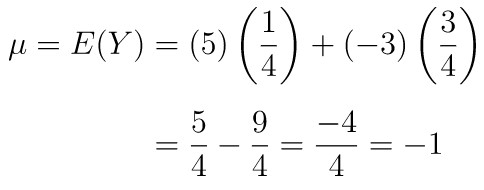
Dalam taruhan ini si pemain rata-ratanya akan kalah Rp1 per lantunan 3 uang logam. Suatu permainan dianggap ‘adil’ bila si pemain, rata-ratanya, tidak menang ataupun kalah; yaitu bila harapan kemenangannya nol (kekalahan dianggap kemenangan yang negatif).
CONTOH 3: Kasus Kontinu
Misalkan \(X\) peubah acak yang menyatakan umur sejenis bola lampu (dalam jam) di mana fungsi kepadatan peluang dari \(X\) (probability density function) diberikan oleh

Hitunglah harapan umur jenis bola lampu tadi.
Penyelesaian:
Dengan menggunakan definisi nilai harapan untuk peubah acak kontinu, diperoleh hasil berikut:

Jadi, jenis bola lampu tadi dapat diharapkan secara rata-rata berumur 200 jam.
TEOREMA 1:
Misalkan \(X\) suatu peubah acak dengan distribusi peluang \(f(x)\). Rataan atau nilai harapan peubah acak \(g(X)\) yang bergantung pada \(X\) adalah

CONTOH 4:
Misalkan peubah acak \(X\) menyatakan banyaknya mobil yang masuk ke suatu pencuci mobil setiap hari antara jam 13.00 - 14.00 dengan distribusi peluangnya yaitu:

Misalkan \(g(X) = 2X – 1\) menyatakan upah, dalam ribuan rupiah, para karyawan yang dibayar perusahaan dalam jam tersebut. Cari harapan pendapatan karyawan pada jam tersebut.
Penyelesaian:
Menurut Teorema 1 di atas, harapan pendapatan para karyawan tersebut adalah

CONTOH 5:
Misalkan \(X\) adalah suatu peubah acak dengan fungsi kepadatan peluang sebagai berikut:
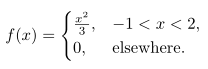
Hitunglah nilai harapan \(g(x) = 4X + 3\).
Penyelesaian:
Menurut Teorema 1 diperoleh

Nilai Harapan dari Kombinasi Linear Peubah Acak
Sekarang dibahas beberapa sifat yang berguna untuk menyederhanakan perhitungan rataan dan variansi peubah acak. Sifat tersebut tersebut memungkinkan kita menyatakan rataan dalam parameter lain yang diketahui ataupun mudah menghitungnya. Semua hasil ini berlaku untuk peubah acak diskret maupun kontinu.
TEOREMA 2:
Bila \(a\) dan \(b\) adalah konstanta, maka
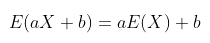
Bukti: (diberikan yang kontinu saja, untuk yang diskret bisa dibuktikan dengan cara yang sama)
Menurut definisi nilai harapan,

Integral pertama di sebelah kanan adalah \(E(X)\) dan integral kedua sama dengan 1. Jadi, diperoleh
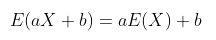
Akibat 1. Bila diambil \(a = 0\) maka \(E(b) = b\).
Akibat 2. Bila diambil \(b = 0\) maka \(E(aX) = a E(X)\)
CONTOH 6:
Dengan menggunakan Teorema 2 untuk peubah acak diskret \(g(X) = 2X -1\), kerjakan kembali Contoh 4.
Penyelesaian:
Menurut Teorema 2, dapat ditulis

Sekarang
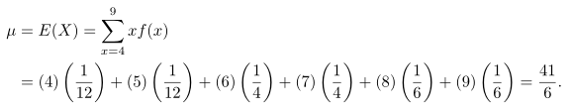
Jadi,
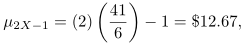
sama seperti sebelumnya.
CONTOH 7:
Dengan menggunakan Teorema 1 untuk peubah acak kontinu \(g(X)=4X+3\), kerjakan kembali Contoh 5.
Penyelesaian:
Pada Contoh 5 kita dapat menggunakan Teorema 2 sehingga diperoleh

Sekarang
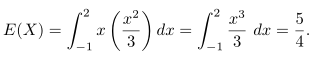
Jadi,
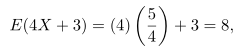
sama seperti sebelumnya.
TEOREMA 3:
Jumlah nilai harapan atau selisih dua atau lebih fungsi suatu peubah acak X sama dengan jumlah atau selisih nilai harapan fungsi tersebut, yaitu
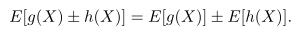
Bukti:
Menurut definisi

CONTOH 8:
Misalkan X peubah acak dengan distribusi peluang sebagai berikut:

Cari nilai harapan \(Y=(X-1)^2\)
Penyelesaian:
Dengan menggunakan Teorema 3 pada fungsi \(Y=(X-1)^2\) maka diperoleh

Dari Akibat 1 Teorema 2, \(E(1) = 1\), dan dengan menghitung langsung

Jadi,

CONTOH 9:
Pembelian mingguan teh botol, dalam ribuan liter, dari suatu agen daerah berbentuk suatu peubah acak kontinu \(g(X)=X^2+X-2\), bila X mempunyai fungsi padat

Carilah nilai harapan \(g(X)=X^2+X-2\).
Penyelesaian:
Menurut Teorema 3, dapat ditulis

Dari Akibat 1 Teorema 2, \(E(2) = 2\), dan dengan menghitung langsung

Sekarang

Jadi, rata-rata pembelian mingguan teh botol dari agen ini sebanyak 2.500 liter.
Artikel Terkait
I have decided to stick with love. Hate is too great a burden to bear.
