Teori Peluang   »   Distribusi Peubah Acak Kontinu   ›  Distribusi Eksponensial

Peubah Acak Kontinu

Distribusi Eksponensial

Distribusi eksponensial mempunyai banyak nilai praktis, terutama dalam hal yang berhubungan dengan waktu, misalnya: waktu tunggu, waktu hidupnya suatu alat atau lamanya jangka waktu sampai suatu alat berhenti berfungsi, lamanya percakapan telepon, dan sebagainya.

---

Distribusi Eksponensial termasuk distribusi kontinu dan merupakan bentuk khusus dari distribusi gamma dengan \(α=1\). Berikut ini adalah beberapa karakteristik penting dari distribusi eksponensial.

• Distribusi eksponensial merupakan distribusi kontinu
• Distribusi eksponensial merupakan keluarga distribusi (family distributions)
• Kurva distribusi eksponensial adalah menceng atau condong ke kanan (perhatikan kurva distribusi eksponensial pada Gambar 1 di bawah)
• Nilai \(x\) (peubah acak yang berdistribusi eksponensial) berkisar dari nol sampai tak hingga
• Puncak kurva distribusi eksponensial selalu di \(x = 0\).
• Kurva distribusi eksponensial akan terus menurun ketika \(x\) semakin besar.

Distribusi eksponensial dapat ditandai dengan satu parameter, yakni \(θ\). Setiap nilai unik \(θ\) menentukan distribusi eksponensial yang berbeda yang mana menghasilkan keluarga distribusi eksponensial.

Gambar 1 di bawah menunjukkan grafik distribusi eksponensial untuk empat nilai parameter \(θ\) yang berbeda dan berbagai nilai \(x\). Berdasarkan bentuk distribusi eksponensial pada definisi di atas, maka rata-rata (mean) dari distribusi eksponensial adalah \(\mu=θ\) dan variannya yaitu \(σ^2=θ^2\).

Gambar 1. Distribusi eksponensial dengan parameter berbeda

Rataan dan Varians

Perlu diingat bahwa rumus rata-rata dan varians di atas berlaku jika fungsi kepadatan peluang (fungsi pdf) dari distribusi eksponensial adalah dalam bentuk scale parameter (1/θ), yakni

Alih-alih menggunakan scale parameter, beberapa buku mungkin akan menuliskan fungsi pdf distribusi eksponensial dalam bentuk rate parameter dengan λ, yakni

\[ f(x;λ) = \begin{cases} λ e^{-λx}, &\quad x > 0, \ λ > 0 \\[1em] 0, &\quad x \ \text{lainnya} \end{cases} \]

Apabila dinyatakan dalam rate parameter, maka rata-rata dan varians dari distribusi eksponensial, yaitu:

\[ \mu = \frac{1}{\lambda} \quad \text{dan} \quad σ^2 = \frac{1}{\lambda^2} \]

Untuk pembuktian rataan dan varians dari suatu peubah acak yang berdistribusi eksponensial, klik link berikut: Rataan dan Varians Distribusi Eksponensial

Hubungan Distribusi Eksponensial dan Poisson

Dalam prakteknya, penggunaan distribusi eksponensial sama pentingnya dengan distribusi Poisson. Dalam distribusi Poisson, peubah acak \(X\) menyatakan banyaknya kejadian (event) dalam interval waktu tertentu (jam, menit, dsb). Sedangkan, dalam distribusi eksponensial, peubah acak \(X\) menyatakan lamanya waktu antara 2 kejadian yang berturut-turut.

Dengan kata lain, variabel acak eksponensial adalah lamanya waktu (\(T\)) dalam satu kejadian Poisson. Oleh sebab itu, terdapat hubungan antara distribusi poisson dan distribusi eksponensial. Jika distribusi Poisson mempunyai parameter \(λ\) dan distribusi eksponensial memiliki parameter \(θ\), maka \(λ=1/θ\).

Distribusi eksponensial mempunyai banyak nilai praktis, terutama dalam hal yang berhubungan dengan waktu, misalnya: waktu tunggu, waktu hidupnya suatu alat atau lamanya jangka waktu sampai sesuatu alat berhenti berfungsi, lamanya percakapan telepon, dan sebagainya.

Moment Generating Function (MGF)

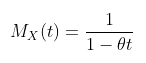
Untuk pembuktian MGF distribusi eksponensial dan cara mencari nilai harapan \(X\) dan varians menggunakan MGF, klik link berikut: MGF Distribusi Eksponensial

Demikian penjelasan terkait peubah acak kontinu yang berdistribusi eksponensial. Terima kasih telah membaca artikel ini sampai selesai. Semoga bermanfaat.

Sumber:

Black, Ken. 2010. Business Statistics For Contemporary Decision Making, 6th ed. John Wiley & Son, Inc. United States of America.

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.