Teori Peluang   »   Pembuktian MGF   ›  MGF Distribusi Chi-Square

MGF Peubah Acak

MGF Distribusi Chi-Square

Pada artikel ini kita akan membahas tentang fungsi pembangkit momen (MGF) dari suatu peubah acak yang berdistribusi chi square dan bagaimana mencari rataan dan varians dari distribusi tersebut berdasarkan fungsi pembangkit momennya.

Distribusi Chi-Square banyak digunakan dalam bidang statistika. Beberapa manfaat dari distribusi Chi-square seperti menguji signifikansi antara frekuensi yang diamati dengan frekuensi teoritis dan menguji kebebasan antar faktor pada tabel kontingensi.

Peubah acak kontinu \(X\) berdistribusi chi-square, dengan derajat bebas \(v\), bila fungsi padatnya diberikan oleh

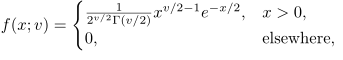
dengan \(v\) bilangan bulat positif.

MGF Distribusi Chi-Square

MGF Distribusi Chi-Square diberikan oleh

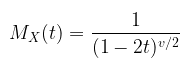
Bukti:

Kita tahu bahwa MGF suatu distribusi diperoleh dari \(E(e^{tX})\). Dengan demikian, MGF dari distribusi chi-square dapat diperoleh sebagai berikut:

Mencari Rataan dan Varians Menggunakan MGF

Seperti yang telah kita pelajari bahwa rataan dan varians suatu peubah acak \(X\) dapat dicari jika diketahui fungsi pembangkit momennya. Untuk mencari rataan dari distribusi chi-square, kita hanya perlu menurunkan fungsi MGF yang telah diperoleh di atas, kemudian menetapkan nilai 0 untuk \(t\). Kita peroleh sebagai berikut:

Untuk mendapatkan varians, kita perlu mencari nilai harapan \( X^2 \) terlebih dahulu. Ini dapat dilakukan dengan mencari turunan kedua fungsi MGF, kemudian menetapkan nilai 0 untuk t. Kita dapatkan hasil berikut ini.

Dengan demikian, varians dari distribusi chi-square adalah sebagai berikut.

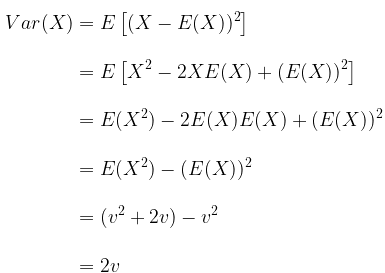
Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.