Teori Peluang   »   Pembuktian MGF   ›  MGF Distribusi Uniform Diskrit

MGF Peubah Acak

MGF Distribusi Uniform Diskrit

Pada artikel ini kita akan membahas fungsi pembangkit momen dari distribusi uniform diskrit dan mencari rataan dan varians dari distribusi tersebut berdasarkan fungsi pembangkit momennya.

---

Distribusi peluang diskret yang paling sederhana ialah yang peubah acaknya memperoleh semua nilainya dengan peluang yang sama. Distribusi peluang semacam itu disebut distribusi seragam (uniform) diskret.

Bila peubah acak \(X\) mendapat nilai \(x_1,x_2,…,x_n\) dengan peluang yang sama, maka distribusi seragam diskret diberikan oleh

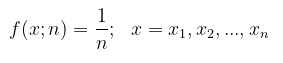
Lambang \(f(x;n)\) dipakai sebagai pengganti \(f(x)\) untuk menunjukkan bahwa distribusi seragam tersebut bergantung pada parameter \(n\).

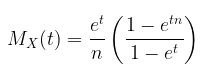
Bukti:

Kita tahu bahwa MGF suatu distribusi didefinisikan sebagai \(E(e^{tX})\). Dengan demikian, MGF dari distribusi uniform diskrit dapat diperoleh sebagai berikut:

Dengan menggunakan rumus deret geometrik, persamaan di atas dapat dijabarkan menjadi

Persamaan di atas dapat disederhanakan dengan menggunakan rumus jumlah deret geometrik. Kita tahu rumus deret geometrik yaitu

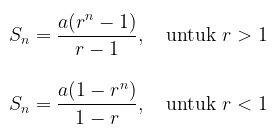
Dalam kasus kita, \(a = \frac{e^t}{n}, r=e^t\) dan karena \(e^t < 1\) maka kita memakai rumus yang kedua pada rumus deret geometrik di atas, sehingga diperoleh

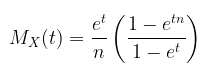
Mencari Rataan dan Varians Menggunakan MGF

Sebagaimana telah kita pelajari bahwa rataan dan varians dari distribusi uniform diskrit, yaitu:

atau bisa juga dinyatakan dengan

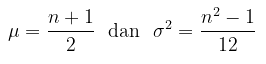
Kita dapat mencari rataan dan varians distribusi uniform diskrit ketika fungsi pembangkit momennya diketahui. Untuk mendapatkan rataan distribusi uniform diskrit, kita perlu mencari turunan pertama dari fungsi MGF terhadap \(t\) dan kemudian menetapkan nilai 0 untuk \(t\). Kita peroleh hasil berikut.

Untuk mendapatkan varians, kita perlu mencari nilai harapan \( X^2 \) terlebih dahulu. Ini dapat dilakukan dengan mencari turunan kedua fungsi MGF, kemudian menetapkan nilai 0 untuk t. Kita dapatkan hasil berikut ini.

Dengan demikian, varians dari distribusi uniform diskrit adalah sebagai berikut.

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.