www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Peubah Acak › PDF dan CDF Peubah Acak Kontinu
Peubah Acak
PDF dan CDF Peubah Acak Kontinu
Peubah acak kontinu X mempunyai nilai setiap bilangan riil serta banyaknya tidak terbatas/tak terhitung. Pada peubah acak kontinu, penghitungan nilai peluang hanya pada suatu titik tertentu tidak mempunyai arti sama sekali.
Jika pada peubah acak diskrit X, nilai-nilai peubah hanya terbatas pada nilai-nilai tertentu, sertanya banyaknya pun terbatas, maka pada peubah acak yang kontinu adalah sebaliknya. Peubah acak kontinu X mempunyai nilai setiap bilangan riil yang termasuk dalam \(Rx\) tertentu, serta banyaknya tidak terbatas/tak terhitung.
Jika X menyatakan umur suatu lampu pijar yang diketahui paling pendek 100 jam dan paling lama 200 jam, maka nilai X dapat berupa sembarang bilangan riil yang memenuhi, yaitu \(100 < x < 200\). Sudah barang tentu banyaknya nilai X tidak terhingga, karena X tidak terbatas pada bilangan bulat.
Pada peubah acak kontinu, penghitungan nilai peluang hanya pada suatu titik tertentu tidak mempunyai arti sama sekali. Nilai peluang ditentukan untuk nilai-nilai X yang terletak dalam interval tertentu. Dengan demikian, jika pada peubah acak diskrit terdapat tabel individual dari nilai peluang, maka pada peubah acak kontinu tidak terdapat tabel semacam itu, yang ada hanya tabel kumulatif.
DEFINISI 1:
Fungsi \(f(x)\) adalah fungsi padat peluang peubah acak kontinu X, yang didefinisikan di atas himpunan semua bilangan real \(R\), bila

CONTOH 1:
Misalkan bahwa galat suhu reaksi, dalam 0C, pada percobaan laboratorium yang dikontrol merupakan peubah acak X yang mempunyai fungsi padat peluang
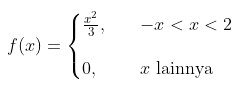
Tunjukkan bahwa syarat 2 pada Definisi 1 terpenuhi dan hitunglah \(P(0 < x ≤ 1)\)!
Penyelesaian:
Untuk kondisi pertama, jelas bahwa \(f(x)≥0\). Untuk kondisi kedua dalam definisi 1, kita peroleh
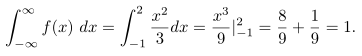
Dengan menggunakan formula 3 dalam definisi 1 diperoleh

DEFINISI 2:
Distribusi kumulatif (tumpukan) \(F(X)\) suatu peubah acak kontinu X dengan fungsi padat \(f(x)\) diberikan oleh

Sebagai akibat langsung Definisi 2 dapat ditulis kedua hasil berikut:

dan

bila fungsi turunan ini ada.
CONTOH 2:
Carilah \(F(x)\) dari fungsi padat pada Contoh 1 dan kemudian hitunglah \(P(0 < X ≤ 1)\).
Penyelesaian:
Untuk \(– 1 < x < 2\),

sehingga

Fungsi distribusi kumulatif \(F(x)\) dalam bentuk grafik disajikan pada Gambar 1. Sekarang,
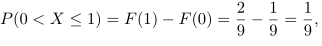
yang mana sesuai dengan hasil yang diperoleh dengan menggunakan fungsi padat di Contoh 1.

Gambar 1 Distribusi kumulatif kontinu
CONTOH 3:
Lamanya percakapan telepon dalam suatu interlokal dapat dianggap sebagai suatu peubah acak kontinu dengan bentuk:

Tentukan:
- Nilai \(β\) hingga \(f(x)\) merupakan pdf dan tentukan pula fungsi cdf nya
- Peluang bahwa seseorang akan melakukan percakapan telepon antara 6 sampai 8 menit.
- Sama dengan (b) tetapi kurang dari 4 menit.
- Sama dengan (b) tetapi lebih dari 5 menit.
Penyelesaian:
- Syarat pdf peubah acak kontinu
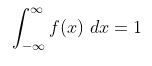
Sehingga

Jadi, fungsi pdf nya adalah

Fungsi CDF nya adalah:


CONTOH 4:
Diketahui suatu peubah acak X mempunyai suatu bentuk fungsi distribusi sebagai berikut:
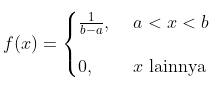
Tentukan fungsi distribusi kumulatifnya.
Penyelesaian:
Fungsi distribusi kumulatifna adalah sebagai berikut:

Oleh karena itu;

CONTOH 5:
Diberikan suatu fungsi kepadatan peluang dari peubah acak X sebagai berikut:

- Tunjukkan bahwa \(f(x)\) adalah fungsi kepadatan peluang.
- Tentukan fungsi distribusi kumulatifnya.
- Carilah \( P\left(-\frac{1}{2} \leq X \leq \frac{2}{3} \right) \).
Penyelesaian:
- Syarat pdf adalah


CONTOH 6:
Buktikan apakah \(f(x)\) merupakan fungsi kepadatan peluang, dan cari \(P(0≤X≤2/3)\) jika diketahui

Penyelesaian:
Kita harus dapat membuktikan bahwa:

Pertama kita cari fungsi kepadatan peluangnya dulu dengan melakukan diferensiasi atau turunan terhadap fungsi cdf.

Jadi, fungsi kepadatan peluangnya adalah \(f(x) = ½\).
Kemudian, baru kita buktikan apakah syarat fungsi pdf nya terpenuhi atau tidak

Karena hasilnya 1, maka syarat fungsi pdf nya terpenuhi.
Sekarang kita akan menghitung peluang \(P(0≤X≤2/3)\).

Artikel Terkait
If A is success in life, then A equals x plus y plus z. Work is x; y is play; and z is keeping your mouth shut.
