Teori Peluang   »   Distribusi Peubah Acak Kontinu   ›  Distribusi Chi-Square

Peubah Acak Kontinu

Distribusi Chi-Square

Distribusi Chi-Square banyak digunakan dalam bidang statistika. Beberapa manfaat dari distribusi Chi-square seperti menguji signifikansi antara frekuensi yang diamati dengan frekuensi teoritis dan menguji kebebasan antar faktor pada tabel kontingensi.

Distribusi khi kuadrat atau chi-square banyak digunakan dalam bidang statistika. Beberapa manfaat dari distribusi khi kuadrat antara lain:

• Menguji perbedaan secara signifikan antara frekuensi yang diamati (frekuensi empiris) dengan frekuensi teoritis
• Menguji kebebasan antar faktor dari data dalam daftar/tabel kontingensi
• Menguji kedekatan data sampel dengan suatu fungsi distribusi seperti binomial, poisson, atau normal.

Mari kita lihat definisi yang lebih formal berikut

Definisi:

Peubah acak kontinu \(X\) berdistribusi chi-square, dengan derajat bebas \(v\), bila fungsi padatnya diberikan oleh

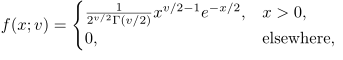
dengan \(v\) bilangan bulat positif.

Distribusi khi kuadrat merupakan bentuk khusus dari distribusi gamma dengan \(α=v/2\) dan \(β=2\), di mana parameter v disebut sebagai derajat kebebasan (degrees of freedom). Nilai derajat kebebasan dapat diperoleh dari banyaknya sampel/observasi dikurangi satu \((n-1)\).

Peluang suatu sampel acak menghasilkan nilai \(χ^2\) lebih besar dari suatu nilai tertentu sama dengan luas di bawah kurva di sebelah kanan nilai tersebut. Nilai tertentu tersebut biasanya dinyatakan dengan \(χ_α^2\). Jadi \(χ_α^2\) menyatakan nilai \(χ^2\) yang di sebelah kanannya terdapat daerah seluas \(α\).

Rataan dan Varians Distribusi Chi-Square

Untuk pembuktian rataan atau nilai harapan dan varians peubah acak chi-square, klik link berikut: Rataan dan Varians Distribusi Chi-Square

Moment Generating Function (MGF) Distribusi Chi-Square

MGF

MGF Distribusi Chi-Square diberikan oleh

Untuk pembuktian MGF dari distribusi chi-square dan cara mencari nilai harapan \(X\) dan varians menggunakan MGF, klik link berikut. MGF Distribusi Chi-Square

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.