www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Konsep Dasar Peluang › Teorema Bayes
Teori Peluang
Teorema Bayes
Teorema Bayes menggambarkan hubungan antara peluang bersyarat dari dua kejadian dan memiliki penerapan yang cukup penting terutama dalam statistika.
Teorema Bayes diambil dari nama penemunya yakni Thomas Bayes yang merupakan seorang ahli statistik, filsuf dan pendeta Inggris. Teorema ini menggambarkan hubungan antara peluang bersyarat dari dua kejadian dan memiliki penerapan yang cukup penting terutama dalam statistika.
TEOREMA 1:
Misalkan kejadian \(B_1,B_2,…,B_k\) merupakan suatu sekatan (partisi) dari ruang sampel \(S\) dengan \(P(B_i )≠0\) untuk \(i = 1, 2, …,k\), maka untuk setiap kejadian A anggota S,

Bukti:
Perhatikan diagram Venn pada Gambar 1. Terlihat bahwa kejadian A merupakan gabungan dari sejumlah kejadian yang saling terpisah
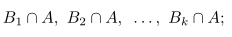
yaitu,
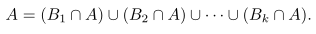

Gambar 1. Penyekatan ruang sampel S
Peluang A kemudian dapat dihitung melalui:
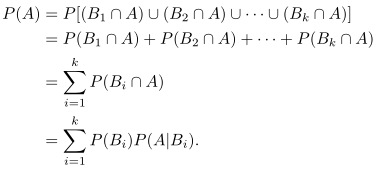
CONTOH 1:
Dalam sebuah pabrik perakitan tertentu, terdapat tiga mesin yaitu mesin B1, B2, dan B2 yang masing-masing membuat 30%, 45% dan 25% dari produk yang dihasilkan. Berdasarkan pengalaman yang lalu bahwa sebanyak 2%, 3% dan 2% dari produks yang dihasilkan masing-masing mesin mengalami cacat. Sekarang, misalnya bahwa sebuah produk yang telah selesai dipilih secara acak. Berapa peluang bahwa produk tersebut cacat?
Pembahasan:
Perhatikan event berikut:
A : produknya cacat
B1: produk yang dibuat mesin B1
B2: produk yang dibuat mesin B2
B3: produk yang dibuat mesin B3
Dengan menerapkan aturan eliminasi (rule of elimination), kita bisa menuliskan

Guna memudahkan pemahaman buatlah sebuah diagram pohon seperti terlihat pada gambar 2 berikut.
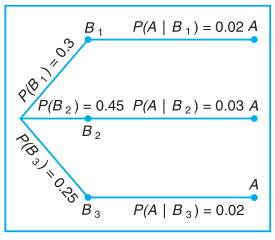
Gambar 2. Diagram pohon Contoh 1
Berdasarkan Gambar 2, kita menemukan bahwa ketiga cabang pada diagram pohon tersebut memberikan peluang:

dan oleh karena itu,

CONTOH 2:
Tiga anggota koperasi dicalonkan menjadi ketua. Peluang Pak Ali terpilih 0,3, peluang Pak Badu terpilih 0,5, sedangkan peluang Pak Cokro 0,2. Kalau Pak Ali terpilih maka peluang kenaikan iuran koperasi adalah 0,8. Bila Pak Badu atau Pak Cokro yang terpilih maka peluang kenaikan iuran adalah masing-masing 0,1 dan 0,4. Berapakah peluang iuran akan naik?
Pembahasan:
Perhatikan kejadian berikut
\(A\): orang yang terpilih menaikan iuran
\(B_1\): Pak Ali yang terpilih
\(B_2\): Pak Badu yang terpilih
\(B_3\): Pak Cokro yang terpilih
Berdasarkan aturan penghapusan maka dapat ditulis

Dengan melihat ke diagram pohon di Gambar 3, terlihat bahwa ketiga cabang mempunyai peluang:
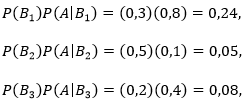
Jadi,

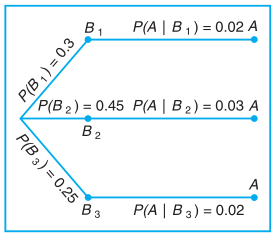
Gambar 3. Diagram pohon untuk Contoh 2
Sebagai ganti menghitung \(P(A)\) menggunakan aturan penghapusan, misalkan sekarang kita cari peluang bersyarat \(P(B_3|A)\) di Contoh 2. Dengan kata lain, bila diketahui bahwa iuran telah naik, berapakah peluangnya bahwa Pak Cokro yang terpilih jadi ketua? Pertanyaan seperti ini dapat dijawab dengan menggunakan teorema berikut, disebut aturan Bayes.
TEOREMA 2:
Misalkan kejadian \(B_1,B_2,…,B_k\) merupakan suatu sekatan ruang sampel S dengan \(P(B_i)≠0\) untuk \(i=1,2,…,k\). Misalkan A suatu kejadian sembarang dalam S dengan \(P(A)≠0\).
Maka,

Bukti:
Menurut definisi peluang bersyarat

dan dengan menyubstitusikan nilai \(P(A)\) yang diperoleh pada Teorema 1 pada penyebut, kita peroleh

Dengan demikian, kita peroleh bentuk

dan buktinya selesai.
CONTOH 3:
Kembali ke Contoh 2, bila seseorang merencanakan masuk jadi anggota koperasi tersebut tapi menundanya beberapa minggu dan kemudian mengetahui bahwa iuran telah naik, berapakan peluang Pak Cokro terpilih jadi ketua?
Dengan menggunakan aturan Bayes dapat ditulis

Dan kemudian masukkan peluang yang telah dihitung di Contoh 2, diperoleh
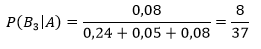
Berdasarkan kenyataan bahwa iuran telah naik, hasil ini menunjukkan bahwa kemungkinan besar bukan Pak Cokro yang sekarang jadi ketua koperasi tersebut.
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
Our character is what we do when we think no one is looking.
