www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Diskrit › Distribusi Geometrik
Peubah Acak Diskrit
Distribusi Geometrik
Distribusi geometrik memiliki ciri bahwa peubah acaknya menyatakan banyaknya percobaan yang diperlukan untuk mendapatkan sukses yang pertama. Distribusi geometrik merupakan kasus khusus distribusi binomial negatif untuk k = 1.
Dalam teori probabilitas dan statistika, distribusi geometrik adalah distribusi yang memiliki ciri bahwa peubah acaknya menyatakan banyaknya percobaan yang diperlukan untuk mendapatkan sukses yang pertama. Distribusi geometrik merupakan kasus khusus distribusi binomial negatif untuk k = 1.
Bila percobaan yang saling bebas dilakukan berulang kali dan menghasilkan sukses dengan peluang \(p\), gagal dengan peluang \(q =1-p\), maka distribusi peluang peubah acak \(X\), yaitu banyaknya usaha sampai saat terjadi sukses yang pertama, diberikan oleh
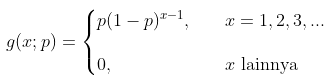
Contoh 1:
Seorang mahasiswa akan menempuh ujian masuk sebuah universitas dan diberi kesempatan untuk menempuh sebanyak 3 kali. Menurut perhitungan dalam tiap ujian ia akan lulus dengan peluang sebesar 60%.
- Berapa persen peluang bahwa ia akan lulus pada ujian yang ketiga
- Berapa persen peluang bahwa dalam 3 kali kesempatan ujian ia akan lulus semua
Penyelesaian:
- Gunakan distribusi geometrik dengan \(x=3\) dan \(p=0,60\), maka diperoleh
- Gunakan distribusi geometrik dengan \(x\leq3\) dan \(p=0,60\), maka diperoleh
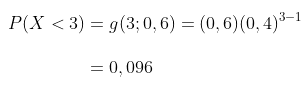

Contoh 2:
Dalam suatu proses produksi diketahui bahwa rata-rata di antara 100 butir hasil produksi 1 yang cacat. Berapakah peluang bahwa setelah 5 butir yang diperiksa baru menemukan cacat pertama?
Penyelesaian:
Gunakan distribusi geometrik dengan \(x =5\) dan \(p = 0,01\), maka diperoleh

Contoh 3:
Pada waktu sibuk suatu sentral telepon hampir mencapai batas daya sambungnya, sehingga orang tidak mendapat sambungan. Ingin diketahui banyaknya usaha yang diperlukan agar mendapat sambungan. Misalkan \(p = 0,05\) peluang mendapat sambungan selama waktu sibuk. Kita ingin mencari peluang bahwa diperlukan 5 usaha agar sambungan berhasil.
Penyelesaian:
Dengan menggunakan distribusi geometrik dengan \(x = 5\) dan \(p = 0,05\) diperoleh

Rataan dan Varians Distribusi Geometrik
Rataan dan Varians Distribusi Geometrik
Rataan dan varians distribusi geoemtrik adalah

Moment Generating Function (MGF) Distribusi Geometrik
MGF Distribusi Geometrik
Fungsi pembangkit momen atau fungsi MGF dari distribusi geometrik adalah

Untuk pembuktian MGF dari distribusi geometrik dan cara mencari nilai harapan, rataan dan varians distribusi geometrik menggunakan MGF, klik link berikut: MGF Distribusi Geometrik
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
Twenty years from now you will be more disappointed by the things that you didn’t do than by the ones you did do.
