www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Kontinu › Distribusi Normal
Peubah Acak Kontinu
Distribusi Normal
Distribusi Normal mengambil peranan penting dalam dunia statistika. Grafiknya disebut kurva normal, berbentuk lonceng, yang menggambarkan dengan cukup baik berbagai gejala yang muncul di alam, industri, dan penelitian.
Distribusi Normal mengambil peranan penting dalam dunia statistika. Grafiknya disebut kurva normal, berbentuk lonceng, yang menggambarkan dengan cukup baik berbagai gejala yang muncul di alam, industri, dan penelitian.
Suatu peubah acak \(X\) yang distribusinya berbentuk lonceng seperti pada Gambar 1 disebut peubah acak normal. Disribusi peluang peubah normal bergantung pada dua parameter \(μ\) dan \(σ\), yaitu rataan dan simpangan bakunya. Jadi, fungsi kepadatan peluang \(X\) akan dinyatakan dengan \(f(x;μ,σ)\). Dalam beberapa literatur, distribusi normal sering disingkat dengan notasi \(n(x;μ,σ)\).
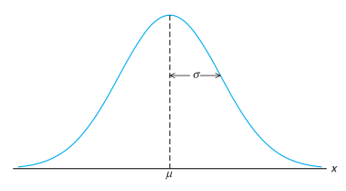
Gambar 1. Kurva normal
Definisi:
Fungsi kepadatan peluang peubah acak normal \(X\), dengan rataan \(μ\) dan varians \(σ^2\), ialah
\[ f(x;μ,σ) = \frac{1}{σ\sqrt{2π}} e^{-\frac{1}{2} \left( \frac{x-μ}{σ} \right)^2}; \quad -∞ < x < ∞ \]
di mana \(π=3,14159…\) dan \(e=2,71828…\)
Begitu \(μ\) dan \(σ\) diketahui maka seluruh kurva normal diketahui. Sebagai contoh, bila \(μ=50\) dan \(σ=5\), maka \(f(x;50,5)\) dapat dengan mudah dihitung untuk berbagai nilai \(x\) dan kurvanya dapat digambarkan.
Pada Gambar 2 ditunjukkan dua kurva normal yang mempunyai simpangan baku yang sama tapi rataannya berbeda. Kedua kurva bentuknya persis sama tapi titik tengahnya terletak di tempat yang berbeda di sepanjang sumbu datar.

Gambar 2. Kurva normal dengan \(μ_1<μ_2\) dan \(σ_1=σ_2\)
Pada Gambar 3 ditunjukkan dua kurva normal dengan rataan yang sama tapi simpangan bakunya berlainan. Terlihat dua kurva mempunyai titik tengah yang sama pada sumbu datar, tapi kurva dengan simpangan baku yang lebih besar tampak lebih rendah dan lebih melebar. Perhatikan bahwa luas di bawah kurva peluang harus sama dengan 1 sehingga bila kumpulan data makin berbeda maka makin rendah dan melebar kurvanya.

Gambar 3. Kurva normal dengan \(μ_1=μ_2\) dan \(σ_1<σ_2\)
Gambar 4 memperlihatkan dua kurva normal yang baik rataan maupun simpangan bakunya berlainan. Jelas keduanya mempunyai letak titik tengah yang berlainan pada sumbu datar dan bentuknya mencerminkan dua nilai \(σ\) yang berlainan.

Gambar 4. Kurva normal dengan \(μ_1<μ_2\) dan \(σ_1<σ_2\)
Dengan mengamati gambar 1 sampai 4 serta memeriksa turunan pertama dan kedua dari \(f(x;μ,σ)\) dapat diperoleh lima sifat kurva normal berikut:
- Modus, titik pada sumbu datar yang memberikan maksimum kurva, terdapat pada \(x=μ\);
- Kurva setangkup terhadap sumbu tegak yang melalui rataan \(μ\);
- Kurva mempunyai titik belok pada x=μ±σ, cekung dari bawah bila \(μ-σ < X < μ+σ\), dan cekung dari atas untuk nilai \(x\) lainnya.
- Kedua ujung kurva normal mendekati asimtot sumbu datar bila nilai \(x\) bergerak menjauhi \(μ\) baik ke kiri maupun ke kanan;
- Seluruh luas di bawah kurva dan di atas sumbu datar sama dengan 1.
Sekarang akan diperlihatkan bahwa parameter \(μ\) dan \(σ^2\) adalah betul rataan dan variansi distribusi normal.
Rataan dan Varians Distribusi Normal
Rataan dan Varians Distribusi Normal
Rataan suatu peubah acak yang berdistribusi normal adalah \(μ\), sedangkan variansnya \(σ^2\)
Untuk pembuktian rataan dan varians peubah acak normal, klik link berikut: Rataan dan Varians Distribusi Normal
Luas di bawah kurva normal
Kurva setiap distribusi peluang kontinu atau fungsi padat dibuat sedemikian rupa sehingga luas di bawah kurva di antara kedua ordinat \(x=x_1\) dan \(x=x_2\) sama dengan peluang peubah acak \(X\) mendapat nilai antara \(x=x_1\) dan \(x=x_2\). Jadi, berdasarkan kurva normal pada Gambar 5, luas daerah yang diwarnai biru dinyatakan sebagai
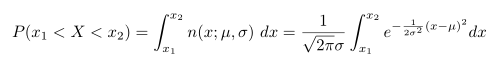
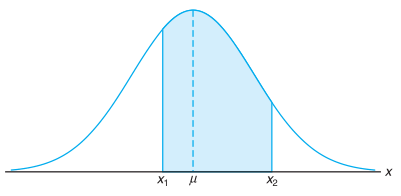
Gambar 5. \(P(x_1 < X < x_2)=\) luas daerah yang diwarnai biru
Untuk mengatasi kesulitan dalam menghitung integral fungsi padat normal maka dibuat tabel luas kurva normal sehingga memudahkan penggunaannya. Akan tetapi, tidak mungkin membuat membuat tabel yang berlainan untuk setiap nilai \(μ\) dan \(σ\). Untunglah, seluruh pengamatan pada peubah acak normal \(X\) dapat ditransformasikan menjadi himpunan pengamatan baru yakni peubah acak normal \(Z\) dengan rataan nol dan variansi 1. Hal ini dapat dikerjakan dengan transformasi \[ Z = \frac{X-μ}{σ} \]
Bilamana \(X\) mendapat suatu nilai \(x\), nilai \(Z\) padanannya diberikan oleh \(z=(x-μ)/σ\). Jadi bila \(X\) bernilai antara \(x=x_1\) dan \(x=x_2\) maka peluang acak \(Z\) akan bernilai antara \(z_1=(x_1-μ)/σ\) dan \(z_2=(x_2-μ)/σ\). Karena itu, dapat ditulis

dengan \(Z\) merupakan suatu peubah acak normal dengan rataan nol dan variansi 1.
Definisi:
Distribusi peubah acak normal dengan rataan nol dan variansi 1 disebut distribusi normal baku.
Distribusi asli dan yang sudah ditransformasi dilukiskan pada Gambar 6. Karena semua nilai \(X\) antara \(x_1\) dan \(x_2\) mempunyai nilai \(Z\) padanan antara \(z_1\) dan \(z_2\), maka luas di bawah kurva \(X\) antara ordinat \(x=x_1\) dan \(x=x_2\) pada Gambar 1 sama dengan luas di bawah kurva \(Z\) antara ordinat \(z=z_1\) dan \(z=z_2\) yang telah ditransformasikan.
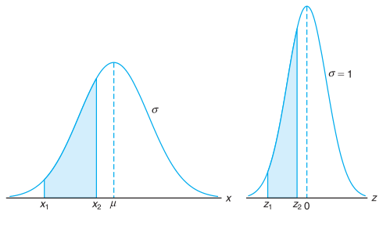
Gambar 6. Distribusi normal asli dan yang telah ditransformasikan
Banyaknya tabel luas kurva normal yang diperlukan dapat diperkecil menjadi satu, yaitu distribusi normal baku. Klik link berikut untuk melihat penggunaan tabel luas kurva normal.
Contoh 1:
Ditentukan distribusi normal baku, carilah luas di bawah kurva yang terletak (a) di sebelah kanan \(z = 1.84\), dan (b) antara \(z = - 1.97\) dan \(z = 0.86\).
Pembahasan:
- Luas pada Gambar 7 (a) di sebelah kanan \(z = 1.84\) adalah 1 dikurangi luas pada tabel kurva normal di sebelah kiri \(z = 1.84\), yaitu \(1- 0.9671 = 0.0329\).
- Luas pada Gambar 7 (b) antara \(z = - 1.97\) dan \(z = 0.86\) sama dengan luas di sebelah kiri \(z = 0.86\) dikurangi luas di sebelah kiri \(z = -1.97\). Dari tabel luar di bawah kurva normal, diperoleh luas yang dicari sebesar \(0.8051 – 0.0244 = 0.7807\).
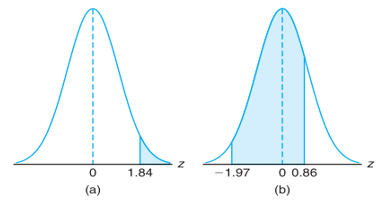
Gambar 7. Kurva normal untuk Contoh 1
Contoh 2:
Ditentukan peubah acak Z berdistribusi normal baku, carilah nilai \(k\) sehingga (a) \(P(Z > k)=0.3015\) dan (b) \(P(k < Z < -0.18)=0.4197\)
Pembahasan:
- Pada Gambar 8 (a) terlihat bahwa nilai \(k\) yang membuat luas sebesar 0.3015 ke sebelah kanan haruslah membuat luas 0.6985 ke sebelah kirinya. Dari tabel luas di bawah kurva normal diperoleh \(k = 0,52\).
- Dari tabel luas di bawah kurva normal, terlihat bahwa jumlah luas di sebelah kiri – 0.18 sebesar 0.4286. Pada Gambar 8 (b) terlihat bahwa luas antara \(k\) dengan – 0.18 adalah 0.4197, jadi luas di sebelah kiri \(k\) haruslah 0.4286 – 0.4197 = 0.0089. Dengan demikian, dari tabel luas di bawah kurva normal diperoleh \(k = - 2.37\).

Gambar 8. Kurva normal untuk Contoh 2
Contoh 3:
Diketahui suatu distribusi normal dengan \(μ=50\) dan \(σ=10\), carilah peluang bahwa \(Z\) mendapat nilai antara 45 dan 62.
Pembahasan:
Nilai \(z\) yang berpadanan dengan \(x_1=45\) dan \(x_2=62\) adalah
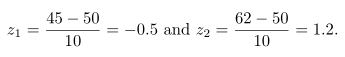
dan

Nilai \(P(-0.5 < Z < 1.2)\) diberikan oleh luas yang diwarnai biru pada Gambar 9. Luas ini dapat dicari dengan mengurangkan luas bagian kiri ordinat \(z = -0.5\) dari seluruh luas bagian kiri \(z = 1.2\). Dengan menggunakan tabel luas di bawah kurva normal, diperoleh


Gambar 9. Daerah untuk Contoh 3
Contoh 4:
Suatu jenis baterai mobil rata-rata berumur 3.0 tahun dengan simpangan baku 0.5 tahun. Bila dianggap umur baterai berdistribusi normal, carilah peluang suatu baterai tertentu akan berumur kurang dari 2.3 tahun.
Pembahasan:
Perhatikan Gambar 10 yang menunjukkan distribusi umur baterai yang diberikan dan luas daerah yang ditanyakan. Untuk menghitung \(P(X<2.3)\), hitunglah luas di bawah kurva normal sebelah kiri titik 2.3.

Gambar 10. Daerah untuk Contoh 4
Ini sama saja dengan menghitung luas daerah sebelah kiri nilai z padanannya. Jadi diperoleh
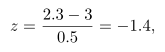
dan kemudian dengan menggunakan tabel luas di bawah kurva normal diperoleh

Contoh 5:
Suatu perusahaan listrik menghasilkan bola lampu yang umurnya berdistribusi normal dengan rataan 800 jam dan simpangan baku 40 jam. Hitunglah peluang suatu bola lampu dapat menyala antara 778 dan 834 jam.
Pembahasan:
Distribusi umur bola lampu dilukiskan pada Gambar 11. Nilai \(z\) yang berpadanan dengan \(x_1=778\) dan \(x_2=834\) adalah
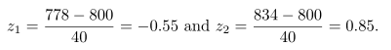
sehingga
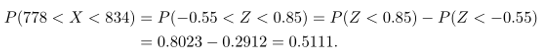

Gambar 11. Daerah untuk Contoh 5
Moment Generating Function (MGF) Distribusi Normal
MGF Distribusi Normal
MGF distribusi normal diberikan oleh
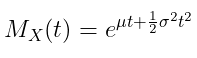
Untuk pembuktian MGF dari distribusi normal dan cara mencari nilai harapan \(X\) dan varians menggunakan MGF, klik link berikut. MGF Distribusi Normal
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
The more you praise and celebrate your life, the more there is in life to celebrate.
