Teori Peluang   »   Pembuktian MGF   ›  MGF Distribusi Uniform Kontinu

MGF Peubah Acak

MGF Distribusi Uniform Kontinu

Pada artikel ini kita akan membahas fungsi pembangkit momen dari distribusi uniform kontinu dan mencari rataan dan varians dari distribusi tersebut berdasarkan fungsi pembangkit momennya.

---

Suatu peubah acak \(X\) pada interval \((a,b)\) dikatakan berdistribusi uniform kontinu jika nilai \(f(x)\) adalah tetap untuk tiap \(x\) dalam interval \((a,b)\) dengan fungsi pdf

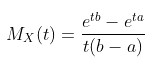
Bukti:

Kita tahu bahwa MGF suatu distribusi diperoleh dari \(E(e^{tX})\). Dengan demikian, MGF dari distribusi uniform kontinu dapat diperoleh sebagai berikut:

Mencari Rataan dan Varians Menggunakan MGF

Sebagaimana telah kita ketahui bahwa rataan dan varians dari distribusi uniform kontinu, yaitu:

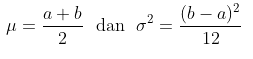
Kita dapat mencari rataan dan varians suatu peubah acak \(X\) jika diketahui fungsi pembangkit momennya. Untuk mencari rataan dari suatu distribusi, biasanya kita menurunkan fungsi MGFnya, kemudian menetapkan nilai 0 untuk \(t\). Namun, ini tidak bisa dilakukan di sini. Perhatikan bahwa turunan pertama MGF Uniform Kontinu adalah

MGF tidak dapat terdefinisikan ketika \(t\) sama dengan nol, namun demikian momen-momen (misalnya momen ke-n) masih bisa dihitung. Kita peroleh momen ke-n distribusi uniform kontinu sebagai berikut.

Dengan demikian,

Sehingga, variansnya adalah

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.