www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Deret Pangkat, Taylor, dan Mac Laurin › Deret Taylor dan Deret MacLaurin - Materi, Contoh Soal dan Pembahasan
Deret
Deret Taylor dan Deret MacLaurin - Materi, Contoh Soal dan Pembahasan
Deret pangkat dari \((x-a)\) yang menggambarkan sebuah fungsi dinamakan deret Taylor. Apabila \(a = 0\), deret yang bersangkutan disebut deret Maclaurin.
Deret Taylor dan Deret MacLaurin merupakan topik yang menarik dalam pembelajaran kalkulus. Kita akan membahas kedua deret tersebut secara mendalam di sini dan memberikan contoh soal penerapannya. Tetapi sebelum itu, saya sarankan Anda memahami apa itu deret pangkat terlebih dahulu.
Misalnya terdapat fungsi \(f(x)\), maka deret taylor dari fungsi \(f(x)\) ini dapat dirumuskan sebagai berikut:
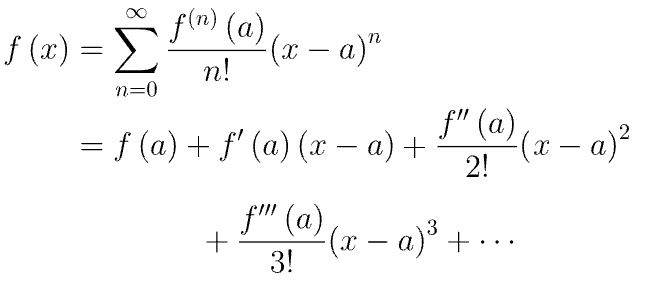
Jika \(a = 0\), atau deret taylor dengan \(x\) di sekitar 0 (\(x = 0\)), maka deret yang diperoleh disebut Deret Maclaurin. Jadi, deret Maclaurin merupakan kasus khusus dari deret Taylor dengan fungsi yang diekspansi di sekitar \(a=0\). Kita tuliskan deret Maclaurin dalam formula berikut:

Sebelum masuk ke contoh soal, ada baiknya kita pelajari darimana rumus Taylor itu diperoleh. Kita mulai dengan memisalkan sebuah fungsi \(f(x)\). Apakah fungsi \(f(x)\) ini dapat diekspansi menjadi sebuah deret pangkat dalam \(x\) atau \(x-a\)? Atau secara lebih spesifik, adakah bilangan-bilangan \(c_0,c_1,c_2,c_3,…\) sehingga
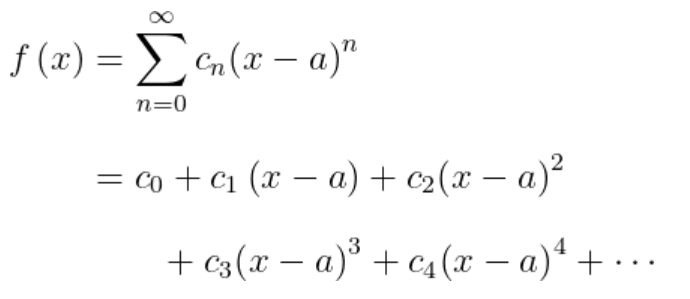
pada sebuah selang sekitar \(x=a\) ?
Andaikan bilangan-bilangan tersebut ada, maka menurut teorema turunan (diferensial), kita peroleh hasil berikut:
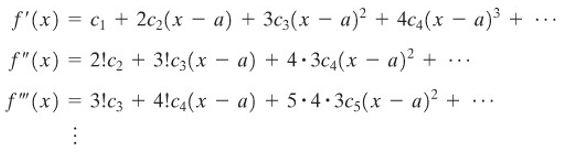
Apabila kita substitusikan \(x = a\) dan menghitung \(c_n\), kita peroleh:

atau secara lebih umum, dapat dituliskan sebagai:
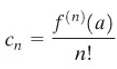
Hasil yang kita peroleh di atas dapat dinyatakan dalam teorema berikut:
Teorema A:
Andaikan \(f(x)\) dapat diekspansi menjadi
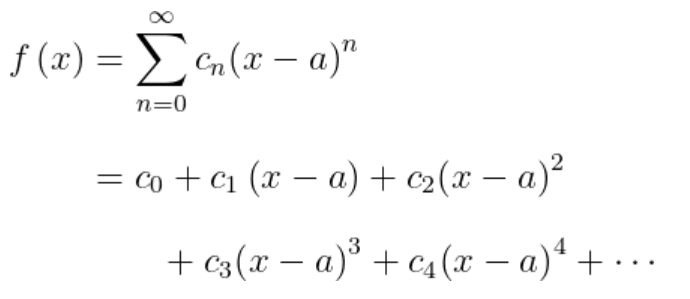
untuk semua \(x\) dalam suatu selang sekitar \(a\). Maka, kita peroleh

Bentuk koefisien \(c_n\) mengingatkan kita pada koefisien yang terdapat dalam Rumus Taylor. Oleh karena ini, deret pangkat dari \((x-a)\) yang menggambarkan sebuah fungsi dinamakan deret Taylor. Apabila \(a = 0\), deret yang bersangkutan disebut deret Maclaurin.
Kekonvergenan Deret Taylor
Walaupun dengan uraian panjang lebar di atas, masih saja ada pertanyaan yang hingga saat ini belum terjawab. Yaitu apabila diketahui sebuah fungsi \(f\), dapatkah kita menggambarkannya sebagai sebuah deret pangkat dalam \(x – a\) (yang tentunya adalah deret Taylor)? Jawabannya ada di dalam teorema berikut.
Teorema B: Rumus Taylor dengan Sisa
Andaikan \(f\) sebuah fungsi yang mana turunan ke-(n+1) yaitu \(f^{n+1}(x)\) ada untuk setiap \(x\) dalam interval terbuka \(I\) yang mengandung \(a\). Maka, untuk setiap \(x\) dalam \(I\),

di mana sisa (atau error) \(R_n(x)\) diberikan oleh rumus:

dan \(c\) adalah titik antara \(x\) dan \(a\) (\(c\) is some point between \(x\) and \(a\)).
Teorema C: Teorema Taylor
Andaikan \(f\) sebuah fungsi yang memiliki turunan dari semua tingkatan dalam suatu selang (\(a- r, a + r\)). Syarat yang perlu dan cukup agar deret Taylor
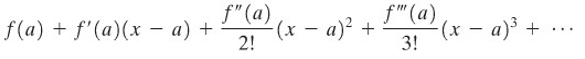
menggambarkan fungsi \(f\) pada selang itu, ialah

dengan \(R_n (x)\) suku sisa dalam Rumus Taylor, yaitu:

dengan \(c\) suatu bilangan dalam selang (\(a-r, a+r\)).
Perhatikan kembali Rumus Taylor pada Teorema B, yaitu:

Apabila \(a = 0\), kita peroleh deret Maclaurin, yakni

Contoh 1:
Tentukan deret Maclaurin untuk \(\sin{x}\) dan buktikan bahwa deret itu menggambarkan \(\sin{x}\) untuk semua \(x\).
Penyelesaian:

Sehingga,

Uraian deret ini akan berlaku untuk semua \(x\), asal dapat dibuktikan bahwa

Sekarang, \(|f^{n+1}(x)|=|\cos{x}|\) atau \(|f^{n+1}(x)|=|\sin{x}|\), sehingga

Tetapi \( \displaystyle{\lim_{n\to\infty} x^n/n! = 0 } \) untuk semua \(x\), karena \(x^n/n!\) merupakan deret konvergen suku ke-n. Akibatnya, kita lihat bahwa \( \displaystyle{\lim_{n\to\infty} R_n(x) = 0 } \).
Contoh 2:
Tentukan deret Maclaurin untuk \(\cos{x}\) dan buktikan bahwa uraian deret itu berlaku untuk semua \(x\).
Penyelesaian:
Kita dapat menggunakan cara yang kita pakai dalam Contoh 1. Tetapi cara yang lebih mudah ialah menurunkan uraian deret dalam Contoh 1, kita peroleh

Contoh 3:
Tentukan deret Maclaurin untuk \(f(x)=\cosh{x}\) dengan dua cara, dan buktikan bahwa uraian itu menggambarkan \(\cosh{x}\) untuk semua \(x\).
Penyelesaian:
Metode pertama ialah metode langsung.
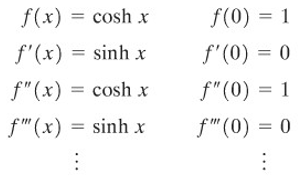
Sehingga,
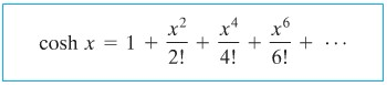
apabila kita dapat membuktikan bahwa \( \displaystyle{\lim_{n\to\infty} R_n(x) = 0 } \) untuk semua \(x\).
Metode 2: Kita gunakan hubungan

Dari pembahasan pada bagian sebelumnya, kita peroleh:
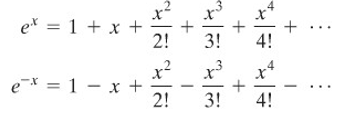
Dengan menjumlahkan dua deret ini, kita peroleh deret pangkat untuk \(\cosh{x}\), setelah jumlah tersebut dibagi dengan 2.
Contoh 4:
Tentukan deret Maclaruin \(\sinh{x}\) dan buktikan bahwa jumlah deret itu menggambarkan \(\sinh{x}\) untuk semua \(x\).
Penyelesaian:
Kita dapat menggunakan cara yang kita pakai dalam Contoh 3. Tetapi cara yang lebih mudah ialah menurunkan uraian deret dalam Contoh 3, kita peroleh:
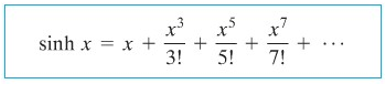
Teorema D: Deret Binomial
Untuk tiap bilangan riil \(ρ\) dan \(|x|<1\) berlaku
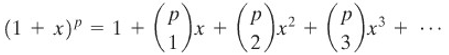
dengan

Apabila \(ρ\) bulat positif, maka \(\binom{\rho}{k} = 0\) untuk \(k > p\), sehingga deret takterhingga itu menjadi sebuah deret suku-suku terhingga. Dalam hal ini deret menjadi suku banyak seperti tercantum dalam Rumus Binomial.
Contoh 5:
Tulislah \((1-x)^{-2}\) sebagai suatu deret Maclaurin pada selang \(-1 < x < 1\).
Penyelesaian:

Sehingga,

Contoh 6:
Tuliskan \( \sqrt{(1+x)} \) sebagai suatu deret Maclaurin dan gunakan hasil ini untuk mengaproksimasi (menghampiri) \( \sqrt{(1,1)} \) sampai 5 angka desimal.
Penyelesaian:
Kita peroleh dengan menggunakan Teorema D.
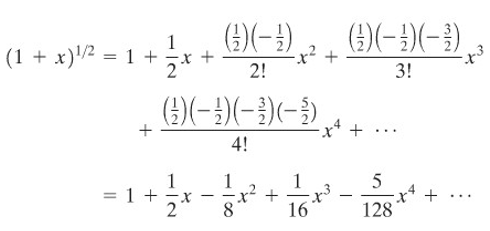
Jadi,

Contoh 7:
Hitunglah \( \int_{0}^{0.4} \sqrt{1+x^4} \, dx \) hingga 5 angka desimal.
Penyelesaian:
Menurut Contoh 6, kita peroleh

Jadi,

Kita simpulkan pembahasan kita tentang deret dengan sebuah daftar deret Maclaurin yang penting yang telah kita dapatkan. Deret-deret ini akan berguna dalam mengerjakan soal-soal tetapi, yang lebih penting lagi, deret-deret ini dapat diterapkan pada banyak persoalan matematika dan ilmu pengetahuan.
Deret Maclaurin yang Penting

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Don’t walk in front of me, I may not follow. Don’t walk behind me, I may not lead. Walk beside me and be my friend.
Albert Camus
