www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Konsep Dasar Peluang › Beberapa Konsep Dasar dalam Peluang
Teori Peluang
Beberapa Konsep Dasar dalam Peluang
Peluang adalah nilai antara nol dan satu yang menggambarkan kemungkinan suatu peristiwa akan terjadi. Peluang bernilai 1 mewakili sesuatu yang pasti akan terjadi, dan peluang bernilai 0 mewakili sesuatu yang tidak dapat terjadi.
Peluang adalah nilai antara nol dan satu yang menggambarkan kemungkinan relatif (relative possibility) suatu peristiwa akan terjadi. Peluang bernilai 1 mewakili sesuatu yang pasti akan terjadi, dan peluang bernilai 0 mewakili sesuatu yang tidak dapat terjadi.
Perhatikanlah apa yang dimaksud dengan pernyatan ‘Ali mungkin memenangkan pertandingan catur’, ‘saya punya peluang setengah mendapatkan bilangan genap dalam lantunan suatu dadu’, ‘kecil kemungkinannya saya menang dalam taruhan itu’.
Beberapa pernyataan di atas merupakan contoh teori peluang yang sering di dengar dalam kehidupan sehari-hari. Dalam tiap pernyataan tersebut dinyatakan hasilnya yang masih diragukan, tetapi menurut pengalaman sebelumnya atau pun dari pemahaman mengenai pola percobaan, kita mempunyai derajat keyakinan mengenai kebenaran pernyataan tersebut.
Peluang atau probabilitas sering dinyatakan sebagai bilangan desimal, seperti 0,70, 0,27, atau 0,50, atau dalam persen seperti 70%, 27% atau 50%. Peluang juga dapat dituliskan dalam bentuk pecahan seperti 7/10, 27/100, atau 1/2. Intinya, nilai peluang bisa berupa nilai berapa pun antara 0 dan 1. Jika dinyatakan sebagai persentase, maka kisarannya antara 0% dan 100%.
Peluang bernilai 1 mewakili sesuatu yang pasti akan terjadi, dan peluang bernilai 0 mewakili sesuatu yang tidak dapat terjadi. Jadi, semakin dekat nilai probabilitas ke 0, semakin tidak mungkin kejadian tersebut akan terjadi. Begitu pula, semakin dekat nilai probabilitas ke 1, semakin besar kemungkinan itu akan terjadi.
Percobaan (Eksperiment), Hasil (Outcome) dan Kejadian (Event)
Terdapat tiga kata kunci yang sering digunakan dalam studi probabilitas: percobaan (experiment), hasil (outcome), dan peristiwa/kejadian (event). Istilah-istilah ini digunakan dalam bahasa kita sehari-hari, tetapi dalam statistik mereka memiliki arti khusus.
Dalam teori peluang (probabilitas), percobaan/eksperimen memiliki dua atau lebih hasil (outcome) yang mungkin, dan kemungkinannya akan terjadi adalah tidak pasti. Sedangkan, hasil (outcome) merupakan hasil tertentu dari sebuah percobaan (a particular result of an experiment).
Sebagai contoh, melempar sebuah koin merupakan suatu percobaan/eksperimen karena memiliki dua hasil yang mungkin (muncul depan atau belakang) dan kita tidak yakin dengan hasilnya. Ketika sebuah koin dilemparkan, satu hasil (outcome) tertentu adalah "depan". Hasil (outcome) lainnya adalah "belakang".
Demikian pula, menanyakan 500 mahasiswa terkait apakah mereka akan bersedia melakukan perjalanan lebih dari 100 mil untuk menghadiri suatu konser merupakan sebuah eksperimen. Dalam eksperimen ini, satu hasil yang mungkin adalah bahwa 273 siswa akan melakukan perjalanan lebih dari 100 mil untuk menghadiri konser. Hasil lain adalah 317 siswa akan menghadiri konser. Hasil lainnya lagi adalah 423 siswa menunjukkan mereka akan menghadiri konser. Ketika satu atau lebih dari hasil eksperimen diamati, kita menyebutnya kejadian/peristiwa (event).
Dengan demikian, kejadian/event dapat didefinisikan sebagai kumpulan dari satu hasil atau lebih dari suatu percobaan (a collection of one or more outcomes of an experiment).
Untuk memperjelas definisi istilah eksperimen/percobaan, hasil (outcome), dan kejadian (event), perhatikan berikut ini.
Dalam percobaan melempar dadu, ada enam kemungkinan hasil (outcome) yakni muncul nilai 1 sampai 6 (untuk dadu yang mempunyai 6 nilai), tetapi ada banyak kemungkinan kejadian (event). Misalnya, kejadian muncul bilangan genap, kejadian muncul bilangan kurang dari 5, kejadian muncul bilangan prima, dan masih banyak lagi kemungkinan yang lain.
Ruang Sampel dan Titik Sampel
Ruang Sampel dan Titik Sampel
Himpunan semua hasil yang mungkin dari suatu percobaan disebut ruang sampel dan biasanya dinyatakan dengan lambang S. Tiap hasil dalam ruang sampel disebut unsur atau anggota ruang sampel tersebut atau biasa disebut juga suatu titik sampel.
Bila ruang sampel mempunyai unsur yang terhingga banyaknya, maka anggotanya dapat didaftar dengan menuliskannya di antara kurang kurawal di mana masing-masing unsur dipisah oleh tanda koma. Jadi, ruang sampel S yang merupakan kumpulan semua hasil yang mungkin dari suatu lantunan mata uang dapat ditulis sebagai

di mana H (head) menyatakan ‘muka’ dan T (tail) “belakang”.
Contoh 1:
Pandanglah suatu percobaan melantunkan sebuah dadu. Bila yang diselidiki ialah nomor yang muncul di sebelah atas, maka ruang sampelnya yaitu

Bila yang ingin diselidiki pada percobaan di atas adalah apakah nomor genap atau ganjil yang muncul, maka ruang sampelnya yaitu

Contoh 1 menunjukkan bahwa hasil suatu percobaan dapat dinyatakan dengan lebih dari satu ruang sampel.
Dalam beberapa percobaan sebaiknya mencatat unsur-unsur ruang sampel secara bersistem dengan menggunakan diagram pohon. Perhatikan contoh berikut ini.
Contoh 2:
Suatu percobaan dilakukan dengan menggunakan sebuah mata uang logam dan sebuah dadu. Pertama, sebuah mata uang logam dilantunkan dan jika hasil yang muncul adalah “muka (head)”, maka mata uang logam tersebut dilantunkan sekali lagi. Akan tetapi, jika ternyata pada lantunan pertama mata uang logam yang muncul adalah “belakang (tail)”, maka sebuah dadu digulirkan sekali.
Untuk mencatat semua unsur ruang sampel yang mungkin, kita buat pohon diagram seperti Gambar 1. Sekarang setiap alur sepanjang cabang pohon itu menyatakan titik sampel yang berlainan. (H = Head = Muka, dan T = Tail = Belakang).

Gambar 1. Diagram pohon untuk Contoh 2
Mulai dari cabang kiri atas dan bergerak ke kanan melalui alur pertama, kita peroleh titik sampel HH, yang menunjukkan kemungkinannya muncul “muka (head)” berturut-turut dalam kedua lantunan uang logam. Demikian pula, titik sampel T3 menunjukkan kemungkinannya uang logam muncul “belakang (tail)” diikuti oleh angka 3 pada guliran dadu. Dengan menelusuri seluruh alur, maka terlihat bahwa ruang sampelnya ialah
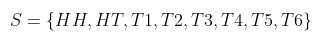
Contoh 3:
Misalkan tiga barang dipilih secara acak dari hasil suatu pabrik. Tiap barang diperiksa dan digolongkan sebagai cacat (D), atau tak cacat (N). Untuk mencatat semua unsur ruang sampel yang mungkin, kita buat diagram pohon seperti pada Gambar 2.

Gambar 2. Diagram pohon untuk Contoh 3 (D = defektif, N = nondefektif)
Sekarang, tiap alur sepanjang cabang pohon itu memberi titik sampel yang berbeda. Mulai dengan alur yang pertama, kita peroleh titik sampel DDD, yang menunjukkan kemungkinan bahwa ketiga barang yang diperiksa cacat. Bila semua alur ditempuh maka kita peroleh ruang sampel sebagai berikut
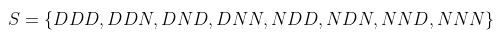
Ruang sampel yang besar atau titik sampelnya berjumlah takhingga lebih mudah ditulis dengan pernyataan atau aturan. Sebagai contoh, bila kemungkinan hasil dari suatu percobaan adalah himpunan kota di dunia yang berpenduduk satu juta, maka ruang sampelnya dapat dituliskan sebagai
S = { x │ x suatu kota yang berpenduduk melebihi satu juta}
dan dibaca ‘S kumpulan semua x, bila x menyatakan kota yang berpenduduk lebih dari satu juta’. Garis tegak yang memisahkan kedua x dibaca ‘bila’ atau ‘jika’.
Contoh 4:
Sebuah mata uang dilantunkan dua kali. Berapakah peluangnya bahwa paling sedikit muncul “muka (head)” sekali?
Pembahasan:
Ruang sampel percobaan ini adalah

Bila mata uang tersebut setangkup, maka tiap hasil mempunyai kemungkinan muncul yang sama. Karena itu tiap titik sampel diberi bobot b sehingga 4b = 1 atau b = ¼. Bila A menyatakan kejadian bahwa paling sedikit satu “muka (head)” muncul, maka A = { HH, HT, TH } dan

Contoh 5:
Suatu dadu diberati sedemikian rupa sehingga kemungkinan muncul suatu angka genap dua kali lebih besar daripada kemungkinan muncul suatu angka ganjil. Bila K menyatakan kejadian munculnya suatu angka yang lebih kecil dari 4 dalam satu lantunan, hitunglah P(K).
Pembahasan:
Ruang sampel T = { 1, 2, 3, 4, 5, 6}. Misalkan bobot tiap angka ganjil b maka bobot tiap angka genap adalah 2b. Karena jumlah semua bobot 1 maka 3b + 3 (2b) = 1 atau 9b = 1 atau b = 1/9. Jadi, tiap angka ganjil berbobot 1/9 sedangkan tiap angka genap berbobot 2/9.
Jadi, K = {1, 2, 3} dan

Bila ruang sampel suatu percobaan berisi N unsur, dan masing-masing dapat terjadi dengan peluang yang sama, maka tiap titik mendapat peluang 1/N. Sedangkan, bila suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan sama, dan bila tepat sebanyak n dari hasil berkaitan dengan kejadian A, maka peluang kejadian A adalah

Contoh 6:
Sekantung permen berisi 6 rasa jeruk, 4 rasa kopi, dan 3 rasa coklat. Bila seseorang mengambil satu permen secara acak, carilah peluangnya mendapat
- satu rasa jeruk, atau
- satu rasa kopi atau coklat.
Pembahasan:
Misalkan J, K, dan C menyatakan kejadian bahwa yang terpilih adalah masing-masing rasa jeruk, kopi atau coklat. Jumlah permen 13 sehingga N = 13, dan semuanya terpilih dengan kemungkinan yang sama.
- Karena 6 dari 13 permen dengan rasa jeruk, maka peluang kejadian J, satu rasa jeruk terpilih secara acak, yaitu
- Karena 7 dari 13 permen dengan rasa kopi atau coklat, maka peluang satu rasa kopi atau coklat yang terpilih secara acak yaitu


Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
The person who reads too much and uses his brain too little will fall into lazy habits of thinking.
