Teori Peluang   »   Distribusi Peubah Acak Kontinu   ›  Distribusi Uniform Kontinu

Peubah Acak Kontinu

Distribusi Uniform Kontinu

Salah satu distribusi yang cukup dikenal adalah apa yang dinamakan distribusi seragam kontinu (continuous uniform) atau kadang cukup disebut distribusi seragam (uniform).

Salah satu distribusi yang cukup dikenal adalah apa yang dinamakan distribusi seragam kontinu (continuous uniform) atau kadang cukup disebut distribusi seragam (uniform). Suatu peubah acak \(X\) pada interval \((a,b)\) dikatakan berdistribusi uniform kontinu jika nilai \(f(x)\) adalah tetap untuk tiap \(x\) dalam interval \((a,b)\) dengan fungsi pdf

Contoh 1:

Jumlah pengunjung dalam suatu gedung pertunjukan diketahui paling sedikit 400 dan paling banyak 600 orang. Dengan menganggap X adalah peubah acak yang menyatakan jumlah pengunjung dan ternyata mempunyai distribusi uniform dalam interval (400,600), maka tentukan peluangnya bahwa:

1. Jumlah pengunjung paling sedikit 550 orang
2. Jumlah pengunjung antara 450 dan 550 orang

Pembahasan:

X mempunyai distribusi uniform dalam interval (400,600)

Dapat juga ditulis sebagai X ~ U(400,600)

Rataan dan Varians Distribusi Uniform Kontinu

Rataan dan Varians

Rataan dan variansi distribusi uniform kontinu adalah

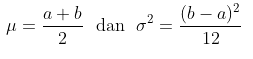
Untuk pembuktian rataan atau nilai harapan dan varians peubah acak uniform kontinu, klik link berikut: Rataan dan Varians Distribusi Uniform Kontinu

Moment Generating Function (MGF) Distribusi Uniform Kontinu

Moment Generating Function

Andaikan \(X\) adalah variabel acak kontinu yang mengikuti distribusi uniform. MGF dari \(X\) diberikan oleh:

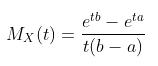
Untuk pembuktian MGF dari distribusi uniform kontinu dan cara mencari nilai harapan \(X\) dan varians menggunakan MGF, klik link berikut. MGF Distribusi Uniform Kontinu

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.