www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Konsep Dasar Peluang › Aturan penjumlahan untuk menghitung peluang
Teori Peluang
Aturan penjumlahan untuk menghitung peluang
Terdapat beberapa aturan penting yang sering dapat menyederhanakan perhitungan peluang, salah satu di antaranya dikenal dengan aturan penjumlahan.
Terdapat beberapa aturan penting yang sering dapat menyederhanakan perhitungan peluang, salah satu di antaranya dikenal dengan aturan penjumlahan yang digunakan dalam gabungan kejadian.
Teorema 1:
Bila A dan B dua kejadian sembarang, maka
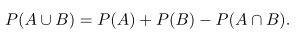
Bukti:
Perhatikan Diagram Venn pada Gambar 1. P(A∪B) adalah jumlah peluang titik sampel dalam A∪B. P(A)+P(B) menyatakan jumlah semua peluang dalam A dan jumlah semua peluang dalam B. Jadi, peluang dalam A∩B telah dijumlahkan dua kali. Karena peluang semua titik dalam A∩B adalah P(A∩B) maka peluang ini harus dikurangkan sekali untuk mendapatkan jumlah peluang dalam A∪B atau P(A∪B).

Gambar 1. Aturan penjumlahan peluang
Akibat 1:
Bila A dan B kejadian yang terpisah, maka \[ P(A \cup B)=P(A)+P(B). \]
Akibat 1 dapat diturunkan langsung dari Teorema 1 karena bila A dan B terpisah maka A∩B=∅ sehingga P(A∩B) = P(∅) = 0.
Akibat 2:
Bila \(A_1,A_2,A_3,…,A_n\) saling terpisah, maka

Akibat 3:
Bila \(A_1,A_2,A_3,…,A_n\) merupakan suatu sekatan (partition) ruang sampel S, maka
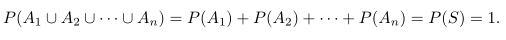
Kita dapat melakukan perluasan untuk Teorema 1 yang dinyatakan dalam teorema berikut.
Teorema 2:
Untuk tiga kejadian A,B, dan C, maka

Contoh 1:
Peluang seorang mahasiswa lulus matematika 2/3 dan peluangnya lulus biologi 4/9. Bila peluangnya lulus kedua mata kuliah adalah ¼, berapakah peluangnya lulus paling sedikit satu mata kuliah?
Pembahasan:
Bila M menyatakan kejadian ‘lulus matematika’ dan B ‘ lulus biologi’, maka menurut Teorema 1 kita peroleh hasil berikut.

Contoh 2:
Berapakah peluangnya mendapatkan jumlah 7 atau 11 bila dua dadu dilantunkan?
Pembahasan:
Misalkan A menyatakan kejadian jumlah 7 muncul dan B menyatakan jumlah 11 yang muncul. Jumlah 7 dapat muncul dalam 6 dari 36 titik sampel dan jumlah 11 dalam 2 titik sampel. Karena semua titik sampel berkemungkinan sama maka P(A)=6/36=1/6 dan P(B)=2/36=1/18. Kejadian A dan B saling terpisah karena jumlah 7 dan 11 tak dapat terjadi pada lantunan yang sama, sehingga

Hasil ini juga dapat diperoleh dengan mencacah banyaknya titik dalam kejadian A∪B, yakni 8, jadi

Contoh 3:
Bila peluang seorang yang membeli mobil akan memilih warna hijau, putih, merah, atau biru, masing-masing, 0,09, 0,15, 0,21, dan 0,23, berapakah peluang seorang pembeli tertentu akan membeli mobil baru berwarna seperti salah satu dari warna tersebut tadi?
Pembahasan:
Misalkan G, W, R, dan B kejadian bahwa seorang pembeli memilih, masing-masing, mobil berwarna hijau, putih, merah dan biru. Karena keempat kejadian ini saling terpisah maka peluangnya sebesar

Sering lebih sulit menghitung peluang bahwa suatu kejadian terjadi daripada menghitung peluang bahwa kejadian tersebut tidak terjadi. Bila hal ini berlaku untuk suatu kejadian A, maka cukup mencari P(A') terlebih dahulu kemudian gunakan Teorema 3 berikut ini. Selanjutnya, cari P(A) dengan pengurangan.
Teorema 3:
Bila A dan A' kejadian yang berkomplementer, maka

Bukti:
Karena \(A \cup A'=S\) dan himpunan \(A\) dan \(A'\) terpisah, maka

Contoh 4:
Bila peluang seorang montir mobil akan memperbaiki 3, 4, 5, 6, 7 atau 8 mobil lebih pada setiap hari kerja yaitu masing-masing sebesar 0,12, 0,19, 0,28, 0,24, 0,10, dan 0,07, berapakah peluang bahwa dia akan memperbaiki paling sedikit 5 mobil pada hari kerja berikutnya?
Pembahasan:
Misalkan E kejadian bahwa paling sedikit 5 mobil yang diperbaiki. Sekarang \(P(E)=1-P(E')\), di mana \(E'\) menyatakan kejadian bahwa kurang dari 5 mobil yang diperbaiki. Karena

maka menurut Teorema 3, kita peroleh hasil berikut:

Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
Guessing is cheap, but guessing wrong can be expensive.
