Teori Peluang   »   Pembuktian Rataan dan Varians   ›  Rataan dan Varians Distribusi Chi-Square

Distribusi Peubah Acak

Rataan dan Varians Distribusi Chi-Square

Distribusi Chi-Square banyak digunakan dalam bidang statistika. Rataan distribusi chi-square diberikan oleh \(E(X) = v\), sedangkan variansnya yaitu \(Var(X) = 2v\).

Distribusi Chi-Square banyak digunakan dalam bidang statistika. Beberapa manfaat dari distribusi Chi-square seperti menguji signifikansi antara frekuensi yang diamati dengan frekuensi teoritis dan menguji kebebasan antar faktor pada tabel kontingensi.

Peubah acak kontinu \(X\) akan berdistribusi chi-square, dengan derajat bebas \(v\), bila fungsi padatnya diberikan oleh

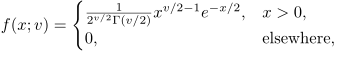
dengan \(v\) bilangan bulat positif.

Bukti: Rataan

Karena distribusi chi-square merupakan hal khusus dari gamma dengan\(α=v/2\) dan \(β=2\), maka rataan dan variansinya dengan mudah dapat dibuktikan. Nilai harapan \(X\) atau rataan dan nilai harapan \(X^2\) distribusi chi-square dapat diperoleh berdasarkan nilai harapan \(X\) dan \(X^2\) distribusi gamma.

Kita tahu bahwa rataan distribusi gamma adalah \( E(X) = αβ \) dan karena \(α=v/2\) dan \(β=2\), maka

Begitu pula, kita tahu bahwa nilai harapan \(X^2\) untuk distribusi gamma adalah

sehingga

Bukti: Varians \(X\)

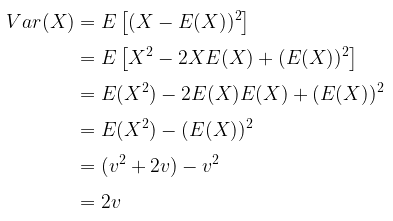
Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.