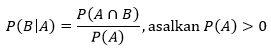
CONTOH 1:

Peluang kakak nonton film kartun sendiri = 0,65; peluang adik nonton film kartun sendiri adalah 0,80. Peluang kakak atau adik nonton film kartun adalah 0,90. Tentukan peluang kakak nonton film kartun jika adik telah nonton terlebih dahulu.

Pembahasan:

Peluang kakak nonton kartun sendiri, \(P(A) = 0,65\)

Peluang adik nonton kartun sendiri, \(P(B) = 0,80\)

Peluang kakak atau adik nonton kartun, \(P(AUB)=0,90\)

Pertama kita cari \(P(A∩B)\) terlebih dahulu:

Peluang kakak nonton film kartun jika adik telah nonton terlebih dahulu adalah peluang A dengan syarat B yaitu

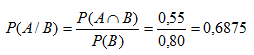
CONTOH 2:

Peluang suatu penerbangan yang telah terjadwal teratur berangkat tepat waktu \(P(B)=0,83\); peluang sampai tepat waktu \(P(S) = 0,82\) dan peluang berangkat dan sampai tepat waktu \(P(B∩S)=0,78\). Cari peluang bahwa pesawat

1. Sampai tepat waktu bila diketahui berangkat tepat waktu,
2. Berangkat tepat waktu jika diketahui sampai tepat waktu.

Pembahasan:

1. Peluang pesawat sampai tepat waktu jika diketahui berangkat tepat waktu

2. Peluang pesawat berangkat tepat waktu bila diketahui sampai tepat waktu

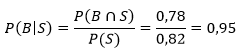
CONTOH 3:

Sebuah dadu dilemparkan 1 kali dan diketahui mata dadu yang muncul adalah ganjil. Tentukan peluang akan muncul mata dadu yang lebih dari 4.

Pembahasan:

Misalkan P(A) menyatakan peluang mata dadu ganjil yang muncul dan P(B) menyatakan peluang muncul dadu lebih dari 4. Dengan demikian, diperoleh hasil berikut.

Jadi, peluang muncul mata dadu lebih dari 4 dan merupakan mata dadu ganjil adalah 1/3.

CONTOH 4:

Seorang siswa memiliki peluang lulus ujian matematika adalah 0,6. Jika ia setelah lulus matematika, maka peluang lulus ujian komputer adalah 0,8. Peluang siswa tersebut lulus ujian matematika dan komputer adalah…

Pembahasan:

Misalkan P(M) menyatakan peluang lulus ujian matematika dan P(K|M) menyatakan peluang lulus ujian komputer setelah lulus matematika. Dengan demikian, diperoleh hasil berikut:

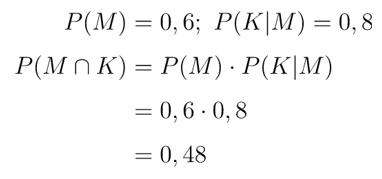
Jadi, peluang siswa tersebut lulus ujian matematika dan komputer adalah 0,48.

CONTOH 5:

Di sebuah daerah, peluang bahwa suatu hari akan berawan adalah 0,4. Diketahui juga bahwa peluang suatu hari berawan dan hujan adalah 0,3. Jika hari ini berawan, peluang bahwa hari ini akan hujan adalah…

Pembahasan:

Misalkan P(A) menyatakan peluang hari ini berawan dan \(P(A∩B)\) menyatakan peluang hari ini berawan dan hujan. Dengan demikian, diperoleh hasil berikut:

Jadi, peluang bahwa hari ini akan hujan jika hari ini berawan adalah ¾.