Teori Peluang   »   Distribusi Peubah Acak Kontinu   ›  Distribusi Student-t

Peubah Acak Kontinu

Distribusi Student-t

Distribusi student-t banyak diterapkan pada statistik inferensia ketika nilai varians dari suatu populasi tidak diketahui.

Distribusi student-t atau kadang hanya disebut distribusi-t banyak diterapkan pada statistik inferensia ketika nilai varians dari suatu populasi tidak diketahui. Untuk sampel yang besar, nilai varians populasi \(σ^2\) dapat diestimasi dengan varians dari sampel \(s^2\) sehingga dapat dilakukan pendekatan (approximate) dengan distribusi normal baku.

Namun, jika sampel yang diambil kecil maka distribusi peubah acaknya akan menyimpang jauh dari distribusi normal baku sehingga diperlukan distribusi student-t.

Kita bisa mendefinisikan peubah acak \(T\) yang mengikuti distribusi student-t sebagai rasio dari peubah acak normal baku \(Z\) terhadap peubah acak chi-square \(V\) dengan derajat bebas \(v\).

Definisi:

Misalkan \(Z\) peubah acak normal baku dan \(V\) peubah acak chi-square dengan derajat bebas \(v\). Bila \(Z\) dan \(V\) adalah peubah acak yang independen, maka distribusi dari

diberikan oleh

Ini dikenal dengan nama distribusi-t dengan derajat bebas \(v\).

Distribusi \(T\) mirip dengan distribusi \(Z\), keduanya setangkup terhadap rataan nol. Keduanya berbentuk lonceng, tapi distribusi \(t\) lebih berbeda satu sama lain karena nilai \(T\) tergantung pada dua besaran yang berubah-ubah, \(\overline{X}\) dan \(S^2\), sedangkan nilai \(Z\) hanya tergantung pada perubahan \(\overline{X}\) dari sampel ke sampel lainnya. Distribusi \(T\) dan \(Z\) berbeda karena varians \(T\) bergantung pada ukuran sampel \(n\) dan varians ini selalu lebih besar dari 1. Hanya ketika ukuran sampel \(n→∞\), kedua distribusi menjadi sama. Pada Gambar 1 diperlihatkan hubungan antara distribusi normal baku \((v=∞)\) dan distribusi \(t\) untuk derajat bebas 2 dan 5.

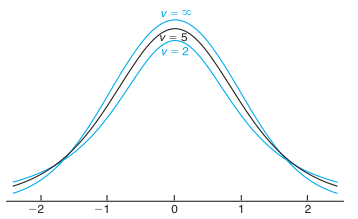
Gambar 1. Kurva distribusi-t untuk \( v=2, 5, \) dan \(∞\)

Peluang suatu sampel acak menghasilkan nilai \(t\) lebih besar dari suatu nilai tertentu atau P(T>t) sama dengan luas di bawah kurva di sebelah kanan nilai tersebut. Nilai tertentu tersebut biasanya dinyatakan dengan \(t_α\) (Perhatikan Gambar 2 di bawah). Jadi \(t_α\) menyatakan nilai \(t\) yang di sebelah kanannya terdapat daerah seluas \(α\). Karena distribusi student-t adalah simetris terhadap rata-rata nol, maka nilai \(t_{1-α}=-t_α\) yaitu nilai \(t\) yang luas daerah di sebelah kanannya \(1-α\) atau luas daerah di sebelah kirinya sebesar \(α\), sama dengan minus nilai \(t\) yang luas bagian kanannya sebesar \(α\).

Gambar 2. Kurva distribusi-t dengan nilai \(t\) tertentu.

Contoh 3:

Cari \(k\) yang memenuhi \(P(k < T < -1.761)=0.045\), untuk sampel acak berukuran 15 yang diambil dari suatu distribusi student-t.

Pembahasan:

Dari tabel distribusi \(t\) terlihat bahwa 1.761 ialah nilai \(t_{0,05}\) bila \(v = 14\). Jadi, \(-t_{0.05}=-1.761\). Karena \(k\) dalam soal ini berada di sebelah kiri dari \(-t_{0.05}=-1.761\) maka ambillah \(k=-t_α\). Selanjutnya, dari Gambar 3 diperoleh \(0.045=0.05-α\) atau \(α=0,005\)

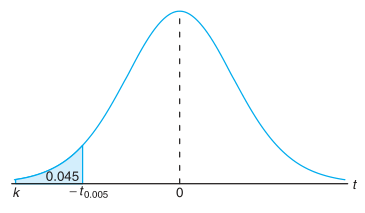
Gambar 3. Nilai \(t\) untuk Contoh 3.

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.