www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Diskrit › Distribusi Hipergeometrik
Peubah Acak Diskrit
Distribusi Hipergeometrik
Distribusi hipergeometrik merupakan salah satu distribusi peubah acak diskrit yang penting. Ahli statistik sering menggunakan distribusi hipergeometrik untuk melengkapi jenis analisis yang dapat dibuat dengan menggunakan distribusi binomial.
Distribusi hipergeometrik merupakan salah satu distribusi peubah acak diskrit yang penting. Ahli statistik sering menggunakan distribusi hipergeometrik untuk melengkapi jenis analisis yang dapat dibuat dengan menggunakan distribusi binomial.
Anda mungkin masih ingat bahwa secara teori, distribusi binomial berlaku hanya untuk percobaan di mana uji coba dilakukan dengan pengembalian (with replacement) (peristiwa independen). Distribusi hipergeometrik hanya berlaku untuk percobaan di mana uji coba dilakukan tanpa pengembalian (without replacement).
Distribusi hipergeometrik, sama sepertinya halnya distribusi binomial, terdiri dari dua hasil yang mungkin yakni sukses dan gagal. Namun, kita harus mengetahui ukuran populasi dan proporsi keberhasilan dan kegagalan dalam populasi untuk menerapkan distribusi hipergeometrik.
Dengan kata lain, karena distribusi hipergeometrik digunakan ketika pengambilan sampel dilakukan tanpa pengembalian, informasi tentang susunan populasi harus diketahui untuk menentukan kembali probabilitas keberhasilan dalam setiap percobaan berturut-turut karena probabilitas berubah.
Dengan demikian, distribusi hipergeometrik memiliki karakteristik sebagai berikut:
- Distribusi hipergeometrik merupakan distribusi diskrit
- Setiap hasil (outcome) terdiri dari keberhasilan atau kegagalan.
- Pengambilan sampel (sampling) dilakukan tanpa pengembalian.
- Populasi (N) adalah terbatas dan diketahui.
- Jumlah keberhasilan dalam populasi, \(k\), diketahui.
Berikut adalah definisi yang lebih formal terkait distribusi hipergeometrik.
Definisi:
Distribusi peluang peubah acak hipergeometrik \(X\), yaitu banyaknya sukses dalam sampel acak ukuran \(n\) yang diambil dari \(N\) benda yang mengandung \(k\) bernama sukses dan \(N-k\) bernama gagal, ialah

Contoh 1:
Dalam suatu gudang terdapat 60 dus obat-obatan di mana diketahui 10 dus di antaranya rusak. Dari gudang tersebut diambil sebanyak 15 dus secara acak. Berapa:
- peluang terdapat 12 dus yang baik?
- peluang paling sedikit terdapat 10 dus yang baik?
- peluang paling banyak terdapat 9 dus yang rusak?
- peluang terdapat antara 5 s/d 10 dus yang baik?
Penyelesaian:
Diketahui bahwa \(N = 60, \ k = 50, \ n = 15\). Dengan demikian, kita peroleh

Contoh 2:
Pada sebuah kontes mencari bakat, peserta yang hadir ada 100 dan diantaranya ada 12 wanita, sisanya adalah laki-laki. Jika diambil 10 orang secara acak, berapa peluang terpilihnya 3 orang wanita?
Penyelesaian:

Contoh 3:
Suatu panitia 5 orang akan dipilih secara acak dari tiga kimiawan dan 5 fisikawan. Hitunglah distribusi peluang banyaknya kimiawan dalam panitian tersebut.
Penyelesaian:
Misalkanlah peubah acak \(X\) menyatakan banyaknya kimiawan dalam panitia. Kedua sifat percobaan hipergeometrik terpenuhi. Jadi,

Berikut disajikan distribusi hipergeometrik \(X\) dalam bentuk tabel

Tidak sulit melihatnya bahwa distribusi peluangnya diberikan oleh rumus

Contoh 4:
Suatu kotak berisi 40 suku cadang dikatakan memenuhi syarat penerimaan bila berisi tidak lebih dari 3 yang cacat. Cara sampling kotak ialah dengan memilih 5 suku cadang secara acak dari dalamnya dan menolak kotak tersebut bila diantaranya ada yang cacat. Berapakah peluang mendapatkan tepat satu yang cacat dalam sampel berukuran 5 bila kotak tersebut berisi 3 yang cacat?
Penyelesaian:
Dengan menggunakan distribusi hipergeometrik untuk \(n =5, \ N = 40, \ k = 3, \) dan \(x = 1\), peluang mendapatkan satu yang cacat adalah

Distribusi Hipergeometrik Peubah Ganda
Bila \(N\) benda dapat dikelompokkan dalam \(k\) sel \(A_1, A_2, …, A_k\) masing-masing berisi \(a_1, a_2,…,a_k\) benda, maka distribusi peluang peubah acak \(X_1,X_2,…,X_k\) yang menyatakan banyaknya benda (anggota) yang terambil dari \(A_1,A_2,…,A_k\) dalam suatu sampel acak ukuran \(n\) ialah
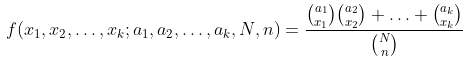
dengan

Contoh 5:
Sejumlah 10 orang dipakai dalam suatu kasus penelitian biologi. Tiga di antara mereka bergolongan darah O, 4 bergolongan A, dan 3 bergolongan B. Berapakah peluang suatu sampel acak ukuran 5 beranggotakan 1 orang bergolongan darah O, 2 bergolongan A, dan 2 lainnya bergolongan B?
Penyelesaian:
Dengan menggunkan perluasan distribusi hipergeometrik di atas untuk

maka peluang yang dicari ialah

Rataan dan Varians distribusi hipergeometrik
Rataan dan Variansi distribusi hipergeometrik \(h(x;N,n,k)\) adalah

Untuk pembuktian rataan dan varians distribusi peubah acak hipergeometrik, klik link berikut: Rataan dan Varians Distribusi Hipergeometrik
Sumber:
Black, Ken. 2010. Business Statistics For Contemporary Decision Making, 6th ed. John Wiley & Son, Inc. United States of America.
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
Let us always meet each other with smile, for the smile is the beginning of love.
