Teori Peluang   »   Peubah Acak   ›  Konsep dan Definisi Peubah Acak

Peubah Acak

Konsep dan Definisi Peubah Acak

Dalam teori peluang konsep peubah acak dan distribusi peluang memegang peranan penting. Peubah acak dinyatakan dengan huruf besar, misalnya \(X\), sedangkan nilainya dinyatakan dengan huruf kecil padanannya, misalnya \(x\).

---

Dalam teori peluang konsep peubah acak dan distribusi peluang memegang peranan penting. Dalam tiap bagian dari teori peluang sering dijumpai kedua istilah tersebut, khususnya penerapan dalam statistika.

Dalam bagian sebelumnya telah dijelaskan bahwa pengertian ruang sampel adalah suatu himpunan/set S yang memiliki anggota semua titik sampel. Pengertian ruang sampel diperlukan sebagai dasar untuk menuju kepada pengertian peubah acak/random variabel dan fungsi distribusi peluang.

Peubah acak bisa didefinisikan sebagai suatu fungsi yang mengaitkan suatu bilangan real pada setiap unsur dalam ruang sampel. Peubah acak dinyatakan dengan huruf besar, misalnya \(X\), sedangkan nilainya dinyatakan dengan huruf kecil padanannya, misalnya \(x\).

Peubah acak juga bisa didefinisikan sebagai sebuah fungsi yang memetakan hasil dari sebuah percobaan acak (random experiment) menjadi nilai numerik. Dengan kata lain, peubah acak merupakan variabel yang nilainya bergantung pada hasil percobaan acak (random/probabilistic experiment). Nilainya tidak diketahui sebelumnya, tetapi nilainya akan diketahui setelah hasil dari percobaannya dilakukan.

Karena peubah acak merupakan hasil dari percobaan acak, maka penting untuk kita memahami apa itu percobaan acak terlebih dahulu.

Percobaan Acak (Random Experiment)?

Sebuah percobaan acak merupakan proses yang mengarah kepada hasil yang tidak pasti (lead to uncertain outcome). Misalnya, saat anda melempar sebuah koin, maka hasil yang muncul bisa berupa Angka atau Gambar. Bahkan jika anda melempar koin tersebut hingga tak terhingga kali hasilnya pasti berupa Angka atau Gambar. Anda tidak akan pernah tahu hasil yang muncul sebelumnya sampai anda melempar koin tersebut dan mendapatkan hasilnya.

Mengapa kita perlu peubah acak? Karena dalam percobaan acak, hasil (outcomes) yang muncul tidak selalu berupa bilangan numerik. Tetapi kita membutuhkan bilangan numerik untuk bisa melakukan penghitungan misalnya menghitung peluang kemunculan 5 Angka dari pelemparan sebuah koin sebanyak 10 kali. Oleh karena itu, kita mendefinisikan sebuah peubah acak sebagai suatu fungsi yang berasosiasi dengan nilai numerik yang unik dengan setiap hasil dari percobaan acak.

Supaya lebih jelas, mari kita mulai dengan contoh pelemparan sebuah koin. Kita menyatakan G apabila muncul gambar dan A apabila muncul angka. Misalnya kita melemparkan koin sebanyak 10 kali, dan hasilnya diberikan berikut ini.

Sekarang kita telah memiliki sebuah sampel yang diperoleh dari pelemparan 10 kali koin. Tetapi, apa yang bisa kita lakukan selanjutnya? Kita tidak bisa melakukan penghitungan apapun karena operasi matematika tidak berlaku dengan baik pada huruf. Salah satu cara yang bisa dilakukan adalah dengan membuat aturan sederhana yaitu mentransformasi huruf ini menjadi sebuah bilangan numerik. Berikut adalah aturannya.

Misalkan kita akan menggunakan sebuah peubah acak X yang mempunyai nilai 1 jika hasil pelemparan koin yang muncul adalah Angka dan mempunyai nilai 0 jika yang muncul adalah Gambar. Dengan demikian, jika diringkas kita peroleh: X = 1 jika yang muncul adalah Angka dan X = 0 jika yang muncul adalah Gambar.

Sehingga hasil dari pelemparan sebanyak 10 kali koin di atas akan menjadi

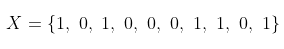
Sekarang misalkan kita ingin menyatakan random variabel X sebagai banyaknya jumlah angka yang muncul dalam pelemparan 10 koin tadi menjadi sebuah nilai numerik. Maka kita akan mendapatkan hasil berikut

X = 0 jika tidak ada angka yang muncul

X = 1 jika ada satu angka yang muncul

X = 2 jika ada dua angka yang muncul

dan seterusnya hingga….

X = 10 jika dalam 10 kali pelemparan koin muncul angka semuanya

Pertanyaan yang kemudian muncul adalah mengapa kita melakukan ini semua? Alasan utama mengapa kita menyatakan peubah acak adalah karena hal itu memungkinkan kita untuk melakukan pertanyaan terhadap sebuah proses acak dalam cara metematika. Jika kita kembali kepada proses acak pelemparan 10 kali koin dan menggunakan peubah acak X yang menyatakan banyaknya angka yang muncul, maka kita dapat dengan mudah menyatakan pertanyaan mengenai proses tersebut seperti ini:

1. P(X=2)
2. P(X<4)
3. P(X>1)

Tiga pertanyaan tersebut setara dengan:

1. Berapa peluang mendapatkan tepat 2 angka?
2. Berapa peluang mendapat kurang dari 4 angka?
3. Berapa peluang mendapatkan lebih dari 1 angka?

Jika kita tidak menggunakan peubah acak maka alternatif lain untuk menyatakan pertanyaan tersebut adalah seperti ini:

1. P(peluang mendapatkan tepat 2 angka jika kita melempar koin sebanyak 10 kali)
2. P(peluang mendapatkan kurang dari 4 angka jika kita melempar koin sebanyak 10 kali)
3. P(peluang mendapatkan lebih dari 1 angka jika kita melempar koin sebanyak 10 kali)

Anda bisa melihat bahwa menggunakan peubah acak tidak hanya memudahkan kita dalam hal penghitungan tetapi juga telah memudahkan kita dalam penulisan.