www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Konsep Dasar Peluang › Kejadian Saling Bebas
Teori Peluang
Kejadian Saling Bebas
Jika terdapat dua kejadian yang saling bebas, maka terjadinya salah satu kejadian tidak memengaruhi kemungkinan terjadinya kejadian yang lain.
Jika terdapat dua kejadian yang saling bebas atau tidak saling bergantung (independen), maka terjadinya salah satu kejadian tidak memengaruhi kemungkinan terjadinya kejadian yang lain. Mari kita lihat pengertian dari dua kejadian yang bebas berikut ini.
DEFINISI 1:
Dua kejadian A dan B bebas jika dan hanya jika
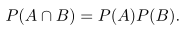
Jadi, untuk mendapatkan peluang bahwa dua kejadian bebas akan terjadi bersama, cukup cari hasil kali peluang kedua kejadian.
Pengertian independen sering dikacaukan dengan pengertian mutually exclusive yang kadang-kadang dianggap sama. Dalam pengertian “independen” kedua kejadian tersebut dapat saja terjadi bersama-sama. Jika A dan B saling bebas, maka:
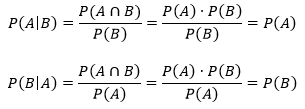
Dengan demikian jika A dan B tidak saling bebas, maka berlaku hubungan:
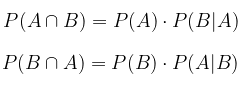
CONTOH 1:
Suatu kota kecil mempunyai satu mobil pemadam kebakaran dan satu ambulans untuk keadaan darurat. Peluang mobil pemadam kebakaran siap waktu diperlukan 0,,98, peluang ambulans siap waktu dipanggil 0,92. Dalam kejadian ada kecelakaan karena kebakaran gedung, cari peluang keduanya siap.
Pembahasan:
Misalkan A dan B menyatakan masing-masing kejadian mobil pemadam kebakaran dan ambulan siap. Maka

CONTOH 2:
Dua dadu dilantunkan dua kali. Berapa peluangnya mendapat jumlah 7 dan 11 dalam dua kali lantunan?
Pembahasan:
Misalkan \(A_1,A_2,B_1\), dan \(B_2\) masing-masing menyatakan kejadian bebas bahwa jumlah 7 muncul dalam lantunan pertama, 7 muncul dalam lantunan kedua, 11 muncul dalam lantunan pertama, dan 11 muncul dalam lantunan kedua. Yang ingin dicari ialah peluang gabungan kejadian \(A_1∩B_2\) dan \(B_1∩A_2\) yang saling terpisah. Jadi,

TEOREMA 1:
Bila dalam suatu percobaan, kejadian \(A_1,A_2,A_3,…,A_k\) dapat terjadi, maka

Bila kejadian \(A_1,A_2,A_3,…,A_k\) saling bebas, maka
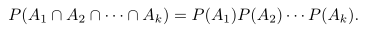
CONTOH 3:
Tiga kartu diambil satu demi satu tanpa pengembalian dari sekotak kartu (berisi 52). Cari peluang bahwa kejadian \(A_1∩A_2∩A_3\) terjadi, bila \(A_1\) kejadian bahwa kartu pertama as berwarna merah, \(A_2\) kejadian kartu kedua 10 atau jack, dan \(A_3\) kejadian kartu ketiga lebih besar dari 3 tapi lebih kecil dari 7.
Pembahasan:
Pertama-tama kita jelaskan lagi kejadian
\(A_1\): kartu pertama as berwarna merah,
\(A_2\): kartu kedua suatu 10 atau jack,
\(A_3\): kartu ketiga lebih besar dari 3 tapi lebih kecil dari 7.
Sekarang

Sehingga menurut Teorema 1,

Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
