www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Diskrit › Pendekatan Distribusi Poisson terhadap Distrbusi Binomial
Peubah Acak Diskrit
Pendekatan Distribusi Poisson terhadap Distrbusi Binomial
Bila \(n\) cukup besar dan \(p\) dekat dengan nol, maka distribusi Poisson dapat digunakan untuk menghampiri distribusi binomial.
Distribusi Poisson dapat dikatakan sebagai bentuk limitnya distribusi binomial di mana nilai \(p→0\) untuk \(n→∞\) dengan \(np\) tetap atau tidak berubah. Arti praktis dari \(p→0\) untuk \(n→∞\) yaitu bahwa untuk \(n\) cukup besar maka nilai \(p\) menjadi kecil.
Yang dimaksud kecil di sini yaitu untuk nilai \(p < 0,05\). Dalam praktek jika \(P < 3 \%\) dan \(n≥40\) maka pendekatan Poisson untuk binomial cukup memadai. Jadi, bila \(n\) besar dan \(p\) dekat dengan nol, maka distribusi Poisson dapat digunakan untuk menghampiri distribusi binomial dengan \(μ=np\).
Teorema:
Misalkan \(X\) peubah acak binomial dengan distribusi peluang \(b(x;n,p)\). Bila \(n→∞, \ p→0\), dan \(np\) tetap sama, maka

Bukti:
Distribusi binomial dapat ditulis sebagai
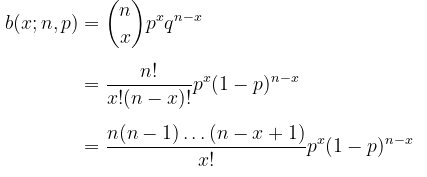
Masukkan \(p=μ/n\), maka diperoleh

Bila \(n→∞\) sementara \(x\) dan \(μ\) tetap, maka

dan dari definisi bilangan \(e\),

Jadi, dengan syarat limit di atas

Contoh 1:
Dalam suatu proses produksi yang menghasilkan barang dari gelas, terjadi gelembung atau cacat yang kadang-kadang menyebabkan barang tersebut sulit dipasarkan. Diketahui bahwa rata-rata 1 dari 1000 barang yang dihasilkan mempunyai satu atau lebih gelembung. Berapakah peluang bahwa dalam sampel acak sebesar 8000 barang akan berisi kurang dari 7 yang bergelembung?
Pembahasan:
Pada dasarnya percobaan ini binomial dengan \(n = 8000\) dan \(p = 0,001\). Karena \(p\) amat kecil dekat dengan nol dan \(n\) cukup besar, maka akan dihampiri dengan distribusi Poisson dengan \(μ=(8000)(0,001)=8\). Jadi, bila \(X\) menyatakan banyaknya barang yang bergelembung, maka
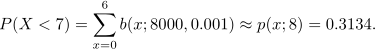
Contoh 2:
Coba selidiki pendekatan Poisson untuk distribusi binomial pada \(n = 45, \ p = 0,04\) untuk \(x = 3\).
Pembahasan:
Diketahui \( μ = np = 1,8 \). Dengan demikian,
\[ f(x=3, μ = 1,8) = P(X=3) = \frac{e^{-1,8}\cdot 1,8^3}{3!} \]
Contoh 3:
Sebuah unit penelitian AD Amerika memproduksi tipe vaksin tertentu sebagai senjata Biokimia. Berdasarkan penelitian diketahui bahwa rata-rata 2 di antara seratus virus tetap hidup selama pemakaian. Berapa peluang bahwa dalam sejumlah vaksin dengan 500 virus,
- setelah pemakaian, terdapat 5 virus hidup?
- paling banyak 5 virus hidup?
- paling sedikit 6 virus hidup?
Pembahasan:
Terdapat 2 di antara 100 virus berarti p = 2% atau 0,02.
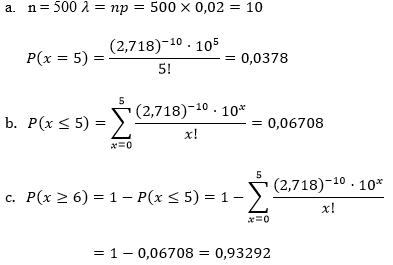
Contoh 4:
Suatu perusahaan lampu listrik memproduksi lampu-lampu pijar. Telah diselidiki, bahwa rata-rata terdapat 4 rusak dari setiap memproduksi 100 lampu.
Perusahaan tersebut mengepak lampu tersebut dalam doos yang berisi 400.
- Berapa kemungkinannya bahwa dalam satu doos tertentu terdapat kurang dari 10 yang rusak?
- Berapa kemungkinannya bahwa dalam doos yang kita pilih terdapat paling sedikit 8 yang rusak?
- Bagaimana kalau yang rusak dalam setiap doos hanya dua buah lampu?
Pembahasan:
Diketahui \(n = 400; \ p = 0,04; \ λ=16\)

Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
The person who reads too much and uses his brain too little will fall into lazy habits of thinking.
