www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Kontinu › Distribusi Fisher
Peubah Acak Kontinu
Distribusi Fisher
Dalam teori probabilitas dan statistika, distribusi F sering kali digunakan dalam pengujian statistika seperti analisis varians dan analisis regresi.
Distribusi \(F\) merupakan salah satu distribusi probabilitas kontinu. Distribusi \(F\) juga dikenal dengan sebutan distribusi \(F\) Snedecor atau distribusi Fisher Snedecor (merujuk pada RA Fisher dan George W. Snedecor).
Dalam teori probabilitas dan statistika, distribusi \(F\) sering kali digunakan dalam pengujian statistika seperti analisis varians dan analisis regresi.
Suatu peubah acak yang mengikuti distribusi \(F\) bisa didefinisikan sebagai rasio dua peubah acak chi-square yang independen, masing-masing dibagi dengan derajat bebasnya (degree of freedom). Jadi, dapat ditulis

di mana \(U\) dan \(V\) menyatakan peubah acak bebas, masing-masing berdistribusi chi-square dengan derajat bebas \(v_1\) dan \(v_2\).
Definisi:
Misalkan \(U\) dan \(V\) dua peubah acak bebas masing-masing berdistribusi chi-square dengan derajat bebas \(v_1\) dan \(v_2\), maka distribusi peubah acak

diberikan oleh
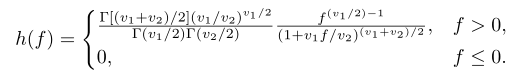
Ini dikenal dengan nama distribusi-F dengan derajat bebas \(v_1\) dan \(v_2\).
Derajat bebas dari peubah acak chi-square pada pembilang \(F\) selalu ditulis lebih dahulu, kemudian diikuti oleh derajat bebas dari peubah acak chi-square yang muncul pada penyebut. Jadi, kurva distribusi \(F\) tidak hanya tergantung pada kedua parameter \(v_1\) dan \(v_2\) tapi juga pada urutan keduanya ditulis. Begitu kedua bilangan ini ditentukan maka kurvanya dapat ditentukan.
Untuk lebih memahami distribusi \(F\), perhatikanlah beberapa plot fungsi kepadatan peluang distribusi \(F\) berikut ini.
Plot 1 – Meningkatkan parameter pertama
Plot berikut berisi grafik dua fungsi kepadatan peluang \(F\):
- Grafik pertama (garis biru) adalah fungsi kepadatan peluang dari peubah acak \(F\) dengan parameter \(v_1=4\) dan \(v_2= 4\);
- Grafik kedua (garis merah) adalah fungsi kepadatan peluang dari peubah acak \(F\) dengan parameter \(v_1=20\) dan \(v_2=4\).
Dengan meningkatkan parameter pertama dari \(v_1=4\) menjadi \(v_1=20\), rata-rata distribusi (yang dinyatakan dengan garis horisontal pada grafik) tidak berubah, tetapi fungsi kepadatannya bergeser dari ekor ke pusat distribusi.

Plot 2 – Meningkatkan parameter kedua
Pada plot berikut di bawah:
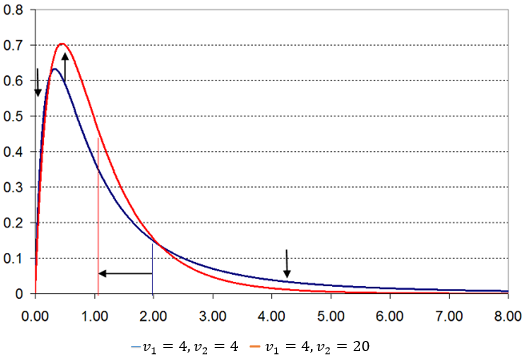
- Grafik pertama (garis biru) merupakan kepadatan distribusi \(F\) dengan parameter \(v_1 = 4\) dan \(v_2 = 4\)
- Grafik kedua (garis merah) merupakan fungsi kepadatan distribusi \(F\) dengan parameter \(v_1=4\) dan \(v_2=20\)
Dengan meningkatkan parameter kedua dari \(v_2=4\) menjadi \(v_2=20\), rata-rata distribusi (yang diwakili oleh garis horisontal pada grafik) menurun (dari 2 menjadi 10/9) dan fungsi kepadatannya bergeser dari ekor (kebanyakan dari ekor kanan) ke pusat distribusi.
Plot 3 – Meningkatkan kedua parameter
Pada plot berikut ini:
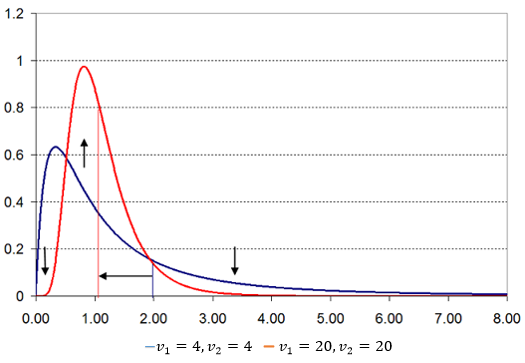
- Grafik pertama (garis biru) merupakan fungsi kepadatan peluang dari peubah acak \(F\) dengan parameter \(v_1=4\) dan \(v_2=4\);
- Grafik kedua (garis merah) merupakan fungsi kepadatan peluang dari peubah acak \(F\) dengan parameter \(v_1=20\) dan \(v_2=20\).
Dengan meningkatkan kedua parameter, rata-rata distribusi menurun (dari 2 menjadi 10/9) dan fungsi kepadatannya bergeser dari ekor ke pusat distribusi. Sebagai akibatnya, distribusinya akan menyerupai bentuk lonceng seperti bentuk pada distribusi normal.
Sekarang mari kita tentukan nilai untuk \(f\) dengan derajat bebas 6 dan 10, yang dilambangkan \(f_α (6,10)\) sehingga luas daerah di sebelah kanannya adalah sebesar \(α\). Ini digambarkan dengan daerah berwarna biru pada gambar di bawah ini.

Untuk mencari nilai \(f\) tersebut anda bisa melihat dari tabel distribusi \(F\) dengan \(α=0.05\). Jadi, nilai \(f\) untuk derajat bebas 6 dan 10, sehingga luas daerah sebelah kanannya sebesar 0.05 adalah \(f_{0.05}=3.22\). Kita juga bisa menghitung nilai \(f_{0.95}\) yang merupakan kebalikan dari \(f_{0.05}\) dan menukar posisi derajat bebasnya seperti terlihat berikut. Jadi nilai \(f\) dengan derajat bebas 6 dan 10 sehingga luas sebelah kanannya 0.95, adalah

Penjelasan di atas memberikan kita teorema berikut ini.
Teorema:
Tulislah \(f_α (v_1,v_2)\) untuk \(f_α\) dengan derajat bebas \(v_1\) dan \(v_2\), maka

Distribusi \(F\) dengan Dua Varians Sampel
Misalkan sampel acak ukuran \(n_1\) dan \(n_2\) diambil dari dua populasi normal masing-masing dengan variansi \(σ_1^2\) dan \(σ_2^2\). Kita tahu bahwa
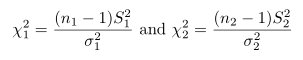
menyatakan dua peubah acak yang berdistribusi chi-square dengan derajat bebas \(v_1=n_1-1\) dan \(v_2=n_2-1\). Selanjutnya, karena kedua sampel diambil secara acak maka kedua peubah acak bebas satu sama lain, sehingga dengan menggunakan definisi distribusi \(F\) di atas, dengan \(χ_1^2=U\) dan \(χ_2^2=V\), diperoleh hasil berikut.
Teorema:
Bila \(S_1^2\) dan \(S_2^2\) variansi sampel acak yang bebas ukuran \(n_1\) dan \(n_2\) yang diambil dari dua populasi

berdistribusi-F dengan derajat bebas \(v_1=n_1-1\) dan \(v_2=n_2-1\).
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
https://www.statlect.com/probability-distributions/F-distribution
Artikel Terkait
A person of high principles is one who can watch an entire chess game without making a comment.
