Teori Peluang   »   Distribusi Peubah Acak Diskrit   ›  Distribusi Bernoulli

Peubah Acak Diskrit

Distribusi Bernoulli

Distribusi Bernoulli bersumber dari percobaan Bernoulli yakni percobaan yang menghasilkan dua kemungkinan hasil - sukses dan gagal.

Distribusi Bernoulli adalah distribusi yang bersumber dari percobaan Bernoulli, yakni suatu percobaan yang menghasilkan dua kemungkinan hasil: Sukses dan Gagal. Contoh sederhana adalah pelemparan sebuah mata uang logam, di mana terdapat 2 kemungkinan hasil yang bisa diperoleh dari satu kali pelemparan, yaitu Angka dan Gambar.

Contoh lain misalnya, pada pengujian barang hasil produksi, dengan tiap pengujian atau usaha dapat menunjukkan apakah suatu barang cacat atau tidak cacat. Kita dapat menentukan atau memilih salah satu hasil sebagai sukses.

Pada pelemparan sebuah mata uang logam, misalkan munculnya Angka dianggap kejadian yang “Sukses” dengan peluang munculnya adalah \(p\) dan munculnya Gambar dianggap kejadian yang “Gagal” dengan peluang munculnya adalah \(1-p\). Selanjutnya, peubah acak \(X\) terkait percobaan tersebut diberi nilai 1 jika “Sukses” terjadi dengan peluang \(p\) dan diberi nilai 0 jika “Gagal” terjadi dengan peluang \(1-p\). Peubah acak \(X\) yang demikian dikatakan berdistribusi Bernoulli.

Fungsi Kepadatan Peluang

Fungsi kepadatan peluang distribusi Bernouli adalah

di mana \(x\) merupakan nilai peubah acak, \(p\) merupakan parameter di mana \(0≤p≤1\). Peubah acak \(X\) yang berdistribusi Bernoulli dapat ditulis \(X \sim Bernoulli(p)\).

Contoh 1:

Pandang suatu kelompok usaha Bernoulli yang berupa pengambilan tiga bahan secara acak dari suatu hasil pabrik, diperiksa, dan kemudian yang cacat dipisahkan dari yang tidak cacat. Bahan yang cacat akan disebut sukses. Banyaknya sukses merupakan suatu peubah acak \(X\) dengan nilai bilangan bulat dari nol sampai 3. Kedelapan hasil yang mungkin (C = cacat, T = takcacat) dan nilai \(X\) adalah

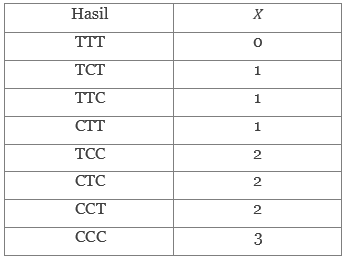
Karena bahan tersebut dipilih secara bebas dari hasil proses yang dianggap menghasilkan 25% bahan yang cacat, maka

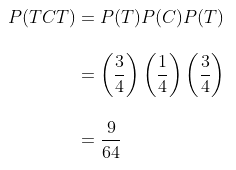
Peluang untuk kemungkinan hasil yang lain dihitung dengan jalan yang sama. Jadi distribusi peluang \(X\) adalah

Rataan dan Varian Distribusi Bernoulli

Untuk pembuktian rataan dan varians peubah acak Bernoulli, klik link berikut: Rataan dan Varians Distribusi Bernoulli

Moment Generating Function (MGF)

MGF Distribusi Bernoulli

Fungsi pembangkit momen atau fungsi MGF dari distribusi Bernoulli yaitu

Untuk pembuktian MGF dari distribusi Bernoulli dan cara mencari nilai harapan \(X\), rataan dan varians menggunakan MGF, klik link berikut. MGF Distribusi Bernoulli

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.