Teori Peluang   »   Distribusi Peubah Acak Kontinu   ›  Distribusi Gamma

Peubah Acak Kontinu

Distribusi Gamma

Distribusi Gamma mendapat namanya dari fungsi gamma, dipelajari dalam banyak bidang matematika. Distribusi gamma yang khusus dengan α = 1 disebut distribusi eksponensial.

---

Distribusi Gamma mendapat namanya dari fungsi gamma yang sudah dikenal luas dan dipelajari dalam banyak bidang matematika. Sebelum membahas distribusi gamma terlebih dahulu akan ditinjau fungsi gamma dan beberapa sifatnya yang terpenting.

Bila dilakukan integral parsial dengan \(μ=x^{α-1}\) dan \(dv=e^{-x} \ dx\) maka diperoleh

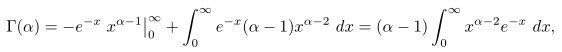
untuk \(α>1\), yang menghasilkan rumus berulang

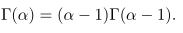
Dengan menggunakan rumus berulang berkali-kali diperoleh

dan seterusnya. Perhatikan bahwa bila \(α=n\), dengan \(n\) bilangan bulat positif, maka

Sekarang fungsi gamma akan dipakai dalam mendefinisikan distribusi gamma.

Grafik beberapa distribusi gamma diperlihatkan pada Gambar 1 untuk beberapa nilai tertentu parameter \(α\) dan \(β\). Distribusi gamma yang khusus dengan \(α=1\) disebut distribusi eksponensial.

Gambar 1. Distribusi gamma

Rataan dan Varians Distribusi Gamma

Moment Generating Function (MGF) Distribusi Gamma

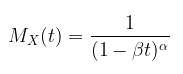
Untuk pembuktian MGF dari distribusi gamma dan cara mencari nilai harapan \(X\) dan varians menggunakan MGF, klik link berikut. MGF Distribusi Gamma

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.