Teori Peluang   »   Pembuktian Rataan dan Varians   ›  Rataan dan Varians Distribusi Binomial Negatif

Distribusi Peubah Acak

Rataan dan Varians Distribusi Binomial Negatif

Distribusi binomial negatif memiliki ciri bahwa peubah acaknya menyatakan banyaknya percobaan yang diperlukan untuk mendapatkan sebanyak \(k\) sukses.

Distribusi binomial negatif memiliki ciri bahwa peubah acaknya menyatakan banyaknya percobaan yang diperlukan untuk mendapatkan sebanyak \(k\) sukses.

Bila usaha yang saling bebas, dilakukan berulang kali dan menghasilkan sukses dengan peluang \(p\) sedangkan gagal dengan peluang \(q =1-p\), maka distribusi peluang peubah acak \(X\), yaitu banyaknya usaha yang berakhir tepat pada sukses ke \(k\), diberikan oleh

Rataan dan Varians Distribusi Binomial Negatif

Rataan dan varians dari distribusi binomial negatif yaitu

Bukti: Rataan

Bukti: Varians

Untuk pembuktiaan varians, kita perlu menentukan nilai harapan \(X^2\) terlebih dahulu. Pertama, misalkan bahwa

Kemudian, carilah nilai E(X(X+1)), yakni:

Sehingga kita peroleh hasil berikut ini:

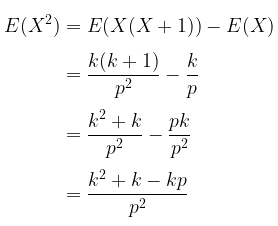
Dengan demikian, variansnya adalah

Cukup sekian penjelasan mengenai rataan dan varians distribusi binomial negatif beserta pembuktiannya dalam artikel ini. Semoga bermanfaat.

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.