www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Peubah Acak › PDF dan CDF Peubah Acak Diskrit
Peubah Acak
PDF dan CDF Peubah Acak Diskrit
Salah satu tujuan penting dari peubah acak adalah untuk menghitung peluang suatu kejadian yang mempunyai nilai tertentu atau yang nilainya terletak dalam interval tertentu.
Salah satu tujuan penting dari peubah acak adalah untuk menghitung peluang suatu kejadian yang mempunyai nilai tertentu atau yang nilainya terletak dalam interval tertentu. \(P(X=x)\) adalah peluang bahwa peubah acak X bernilai X, atau \(P(x_1 < X < x_2)\) adalah peluang peubah acak X bernilai antara \(x_1\) dan \(x_2\).
Sering lebih mudah bila semua peluang suatu peubah acak X dinyatakan dalam suatu rumus. Rumus seperti itu tentunya merupakan fungsi nilai numerik X yang akan dinyatakan dengan \(f(x), g(x), r(x)\), dst. Jadi ditulis \(f(x) = P(X= x)\); yaitu \(f(3) = P(X = 3)\). Himpunan pasangan terurut \((x,f(x))\) disebut fungsi kepadatan peluang atau distribusi peluang peubah acak diskret X.
DEFINISI 1:
Himpunan pasangan terurut \((x,f(x))\) merupakan suatu fungsi peluang, fungsi massa peluang, atau distribusi peluang peubah acak diskret X bila untuk setiap kemungkinan hasil X:
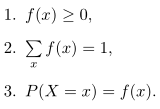
CONTOH 1:
Suatu pengiriman 20 komputer PC yang sama ke suatu toko mengandung 3 yang cacat. Bila suatu sekolah membeli 2 komputer ini secara acak, cari distribusi peluang banyaknya yang cacat.
Penyelesaian:
Misalkan X peubah acak dengan nilai X kemungkinan banyaknya komputer yang cacat yang dibeli sekolah tersebut. Maka X dapat memperoleh setiap nilai 0,1, dan 2. Sekarang,
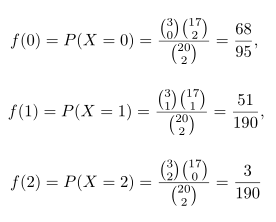
Jadi distribusi peluang X

CONTOH 2:
Diketahui suatu fungsi sebagai berikut.
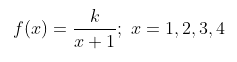
Tentukan k sehingga \(f(x)\) merupakan fungsi kepadatan peluang!
Penyelesaian:
Syarat pdf adalah
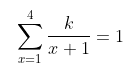
Sehingga

Jadi, fungsi pdf nya adalah

Fungsi kepadatan peluang (pdf) diskrit dapat dinyatakan dalam bentuk notasi fungsi \(f(x)\) yang dapat ditulis dalam bentuk tabel yang menggambarkan nilai-nilai \(f(x)\) untuk tiap X. Bentuk tabel pdf dari contoh di atas adalah

Dalam banyak soal diperlukan menghitung peluang bahwa nilai amatan peubah acak X akan lebih kecil atau sama dengan suatu bilangan real X. Bila \(F(x)=P(X≤x)\) untuk setiap bilangan real X, kita namakan \(F(x)\) sebagai distribusi kumulatif/tumpukan peubah acak X.
DEFINISI 2:
Distribusi kumulatif \(F(X)\) suatu peubah acak diskret X dengan distribusi peluang \(f(x)\) dinyatkan oleh
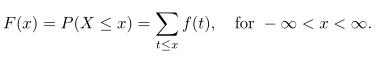
\(F(X)\) merupakan penjumlah dari \(f(x)\) sehingga nilai terkecil dari \(F(x)\) adalah 0 sedangkan nilai terbesarnya adalah 1. Jadi \(0≤F(X)≤1\).
Berdasarkan definisi 2, maka dapat ditunjukkan bahwa:

CONTOH 3:
Bila 50% mobil yang dijual oleh suatu agen bermesin diesel, cari rumus distribusi peluang banyaknya mobil bermesin diesel bagi ke 4 mobil berikutnya yang dijual oleh agen tersebut dan juga hitunglah distribusi kumulatif peubah acak X. Dengan menggunakan \(F(x)\), perlihatkan bahwa \(f(2) = 3/8\).
Penyelesaian:
Karena peluang menjual mobil bermesin diesel atau bensin adalah 0,5, maka ke \( 2^4 = 16 \) titik pada ruang sampel mempunyai peluang yang sama. Jadi, pembagi untuk semua peluang, dan juga untuk fungsi peluang adalah 16.
Umumnya, kejadian menjual x mobil bermesin diesel dan 4-x bermesin bensin dapat terjadi dalam \( \binom{4}{x} \) cara, x bernilai 0, 1, 2, 3, atau 4. Jadi, distribusi peluang \( f(x) = P(X=x) \) adalah
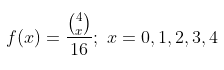
Dari distribusi peluang ini, kita peroleh
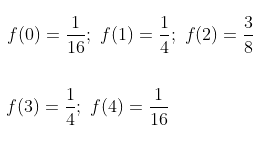
Dengan demikian,
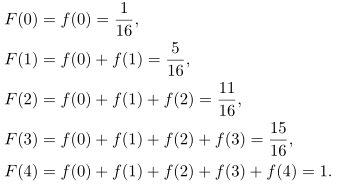
Sehingga

Sekarang
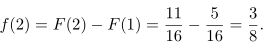
Sering menolong bila distribusi peluang digambarkan dalam bentuk grafik. Titik \((x,f(x))\) dalam Contoh 3 dapat digambarkan seperti pada Gambar 1. Gambar 1 memperlihatkan dengan jelas nilai X yang paling besar kemungkinan nya terjadi, dan dalam kasus ini menunjukkan bentuk yang setangkup sempurna.

Gambar 1 Diagram balok
Orang lebih sering menggambarkan persegi panjang seperti pada Gambar 2 daripada menggambarkan titik \((x,f(x))\) pada Gambar 1. Persegi panjang ini dibuat sedemikian rupa sehingga alasnya yang sama panjang mempunyai titik tengah tiap nilai X dan tingginya sama dengan peluang yang sesuai yang diberikan oleh \(f(x)\). Alasnya dibuat sedemikian rupa sehingga sisi dua persegi panjang yang berdampingan bersatu. Gambar 2 ini disebut histogram peluang.

Gambar 2. Histogram peluang
Grafik distribusi kumulatif Contoh 3 yang merupakan fungsi tangga seperti pada Gambar 3 diperoleh dengan menggambarkan sejumlah titik \((x,F(x))\).

Gambar 3 Distribusi kumulatif diskret
Artikel Terkait
Keep your eyes on the stars and your feet on the ground.
