www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Kontinu › Pendekatan Distribusi Normal terhadap Distribusi Binomial
Peubah Acak Kontinu
Pendekatan Distribusi Normal terhadap Distribusi Binomial
Distribusi normal memberikan hampiran yang amat baik terhadap distribusi binomial bila n besar dan p dekat ke 0 atau 1. Bahkan bila n kecil tapi p cukup dekat ke ½, hampiran normal untuk distribusi binomial masih cukup baik.
Berikut ini diberikan satu teorema yang memungkinkan penggunaan luas di bawah kurva normal untuk menghampiri peluang binomial bila \(n\) cukup besar.
Teorema:
Bila \(X\) peubah acak binomial dengan rataan μ=np dan variansi \(σ^2=npq\) maka bentuk limit distribusi
\[ z = \frac{X-np}{\sqrt{npq}} \]
ketika \(n→∞\), ialah distribusi normal baku \(n(z,0,1)\).
Ternyata distribusi normal dengan \(μ=np\) dan \(σ^2=np(1-p)\) memberikan hampiran yang amat baik terhadap distribusi binomial bila \(n\) besar dan \(p\) dekat ke 0 atau 1. Bahkan bila \(n\) kecil tapi \(p\) cukup dekat ke ½, hampiran normal untuk distribusi binomial masih cukup baik.
Untuk melihat hampiran normal terhadap distribusi binomial, mula-mula dilukiskan histogram \(b(x;15,0.4)\) dan kemudian meletakkan kurva normal dengan rataan dan variansi yang sama dengan peubah binomial \(X\) sehingga keduanya saling tumpang tindih. Untuk itu lukiskanlah kurva normal dengan

Histogram \(b(x;15,0.4)\) dan kurva normal padanannya, yang seluruhnya telah tertentu oleh rataan dan variansinya, dilukiskan pada Gambar 1.

Gambar 1. Hampiran normal terhadap \(b(x;15,0.4)\)
Peluang dari peubah acak binomial \(X\) mendapatkan suatu nilai \(x\) tertentu sama dengan luas persegi panjang yang alasnya mempunyai titik tengah \(x\). Sebagai contoh, peluang bahwa \(X\) nilainya 4 sama dengan luas persegi panjang dengan alas yang titik tengahnya \(x = 4\). Dengan menggunakan tabel binomial, luas tadi adalah
\[ P(X = 4) = b(4;15, 0.4) = 0.1268 \]
Luas ini secara hampiran sama dengan luas daerah yang diberi warna biru di bawah kurva normal antara ordinat \(x_1=3.5\) dan \(x_2=4.5\) pada Gambar 2. Jika diubah ke nilai \(z\), maka diperoleh
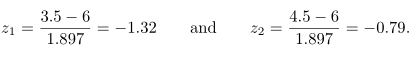

Gambar 2. Hampiran normal terhadap \(b(x;15,0.4)\) dan \(\sum_\limits{x=7}^9 b(x;15,0.4)\)
Bila \(X\) peubah acak binomial dan \(Z\) peubah acak normal baku, maka
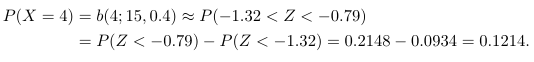
Hasil ini cukup dekat dengan nilai sesungguhnya sebesar 0.1268.
Hampiran normal paling berguna dalam menghitung jumlah binomial untuk nilai \(n\) yang besar. Kembali pada Gambar 2, misalkanlah ingin diketahui peluang bahwa \(X\) mendapat nilai di antara dan termasuk 7 dan 9. Peluangnya diberikan oleh

yang sama dengan jumlah luas bujur sangkar, masing-masing dengan alas yang berpusat di \(x = 7, 8,\) dan 9. Untuk hampiran normal luas tersebut adalah luas daerah yang diberi warna biru antara ordinal \(x_1=6.5\) dan \(x_2=9.5\) pada Gambar 2. Nilai \(Z\) padanannya yaitu
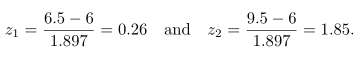
Dengan demikian,
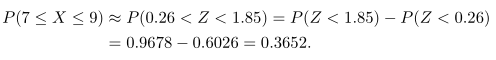
Sekali lagi terlihat bahwa kurva normal memberikan hampiran yang cukup dekat dengan nilai sesungguhnya 0.3564. Derajat ketelitian, yang tergantung pada kecocokan kurva dengan histogram, akan bertambah bila \(n\) membesar. Hal ini khususnya benar bila \(p\) tidak terlalu dekat ke ½ dan histogram tidak lagi setangkup. Gambar 3 dan 4 masing-masing menunjukkan histogram \(b(x;6,0.2)\) dan \(b(x;15,0.2)\). Terlihat bahwa kecocokan kurva normal dengan histogram akan lebih baik bila \(n = 15\) daripada bila \(n = 6\).

Gambar 3. Histogram \(b(x;6,0.2)\)

Gambar 4. Histogram \(b(x;15,0.2)\)
Kesimpulannya, hampiran normal digunakan untuk mengevaluasi peluang binomial apabila \(p\) tidak dekat ke 0 atau 1. Hampiran akan baik bila \(n\) besar dan cukup baik apabila \(n\) kecil dan \(p\) cukup dekat ke ½. Satu kemungkinan panduan yang bisa dipakai untuk menggunakan hampiran normal terhadap binomial yaitu apabila \(np\) dan \(nq\) lebih besar atau sama dengan 5, hampirannya baik.
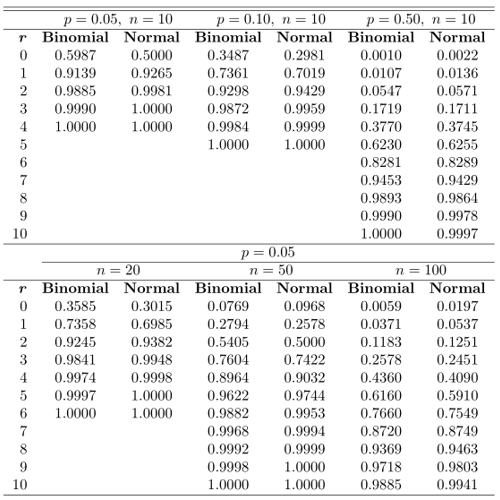
Seperti dikemukan sebelumnya, hampiran akan baik bila \(n\) besar. Bila \(p\) dekat ke ½, ukuran sampel sedang atau kecil mendapatkan hampiran yang cukup baik. Tabel 1 berikut disajikan untuk menunjukkan kualitas hampiran. Baik hampiran normal maupun peluang kumulatif binomial yang sesungguhnya disajikan. Perhatikan bahwa untuk \(p = 0.05\) dan \(p = 0.01\), selisih hampiran cukup besar untuk \(n = 10\). Akan tetapi, kendati \(n = 10\), hampiran menjadi cukup baik untuk \(p = 0.50\) yang terlihat dari selisih hampiran yang kecil. Di sisi lain, bila \(p\) tetap sebesar \(p = 0.05\), perhatikan bahwa hampirannya bertambah baik bila \(n\) bergerak dari 20 menjadi 100.
Tabel 1 Hampiran normal dan peluang binomial kumulatif sesungguhnya
Contoh 1:
Peluang seseorang penderita sembuh dari suatu penyakit darah yang jarang muncul 0.4. Bila diketahui ada 100 orang yang telah terserang penyakit ini, berapa peluangnya bahwa kurang dari 30 yang sembuh?
Penyelesaian:
Misalkan peubah binomial \(X\) menyatakan banyaknya penderita yang sembuh. Karena \(n = 100\), maka penggunaan hampiran kurva normal seharusnya memberi hasil yang cukup tepat dengan
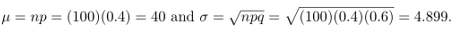
Untuk mendapatkan peluang yang dicari, harus dicari luas di sebelah kiri \(x = 29.5\). Nilai z yang berpadanan dengan 29.5 adalah

dan peluang kurang dari 30 dari 100 penderita yang sembuh diberikan oleh daerah yang diwarnai biru pada Gambar 5. Jadi

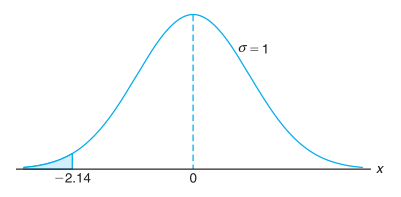
Gambar 6. Daerah untuk Contoh 1
Contoh 2:
Suatu ujian pilihan ganda terdiri atas 200 soal masing-masing dengan 4 pilihan dan hanya satu jawaban yang benar. Tanpa memahami sedikit pun masalahnya dan hanya dengan menerka saja, berapakah peluang seorang murid menjawab 25 sampai 30 soal dengan benar untuk 80 dari 200 soal?
Penyelesaian:
Peluang menjawab benar untuk tiap soal dari 80 adalah \(p = ¼\). Bila \(X\) menyatakan banyaknya jawaban yang benar dengan hanya menerka maka

Dengan menggunakan hampiran kurva normal dengan
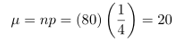
dan
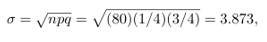
diperlukan luas antara \(x_1=24.5\) dan \(x_2=30.5\). Nilai \(z\) padanannya adalah

Peluang menerka tepat 25 sampai 30 soal diberikan oleh daerah yang diwarnai biru pada Gambar 6. Dari tabel luas di bawah kurva normal, diperoleh


Gambar 6. Daerah untuk Contoh 2
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
There are only two ways to live your life. One is as though nothing is a miracle. The other is as though everything is a miracle.
