Teori Peluang   »   Pembuktian Rataan dan Varians   ›  Rataan dan Varians Distribusi Uniform Diskrit

Distribusi Peubah Acak

Rataan dan Varians Distribusi Uniform Diskrit

Distribusi uniform diskrit adalah distribusi yang peubah acaknya memperoleh semua nilainya dengan peluang yang sama.

---

Distribusi peluang diskret yang paling sederhana ialah yang peubah acaknya memperoleh semua nilainya dengan peluang yang sama. Distribusi peluang semacam itu disebut distribusi seragam (uniform) diskret.

Bila peubah acak \(X\) mendapat nilai \(x_1,x_2,…,x_n\) dengan peluang yang sama, maka distribusi seragam diskret diberikan oleh

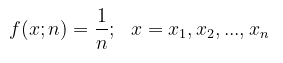
Lambang \(f(x;n)\) dipakai sebagai pengganti \(f(x)\) untuk menunjukkan bahwa distribusi seragam tersebut bergantung pada parameter \(n\).

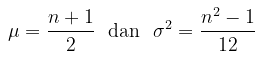
Bukti:

Menurut definisi

Berdasarkan rumus jumlah khusus, maka

Dengan demikian,

Begitu pula, menurut definisi

Mari kita lanjutkan untuk mencari bukti varians yang kedua. Pertama, kita cari \(E(X^2)\) terlebih dahulu.

Berdasarkan definisi rumus jumlah khusus,

Dengan demikian,

Berikutnya, varians kedua dapat dicari dengan rumus

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.