www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Peubah Acak › Menghitung Nilai Harapan dan Varians
Peubah Acak
Menghitung Nilai Harapan dan Varians
Rataan mempunyai peran khusus karena menggambarkan letak pusat suatu distribusi peluang. Namun, rataan tidak memberikan keterangan yang cukup mengenai bentuk distribusinya. Maka itu, diperlukan ukuran lain untuk menggambarkan suatu distribusi peluang, yakni varians.
Rataan suatu peubah acak mempunyai peran khusus dalam statistika karena menggambarkan letak pusat suatu distribusi peluang. Akan tetapi, rataan itu sendiri tidaklah memberikan keterangan yang cukup mengenai bentuk distribusinya.
Pada Gambar 1 tertera histogram dua distribusi peluang diskrit dengan rataan \(μ=2\) yang sama tetapi cukup berbeda dalam keragaman atau pemencaran pengamatannya di sekitar rataan.

Gambar 1. Distribusi dengan rataan yang sama tapi pemencaran berbeda
Ukuran keragaman suatu peubah acak \(X\) dapat diperoleh dengan

Ukuran keragaman ini diberi nama varians peubah acak \(X\) atau varians distribusi peluang \(X\) dan dinyatakan dengan \(Var(X)\) atau \(σ_x^2\). Perhatikan definisi formalnya berikut ini.
DEFINISI:
Misalkan \(X\) peubah acak dengan distribusi peluang \(f(x)\) dan rataan \(μ\). Variansi \(X\) adalah
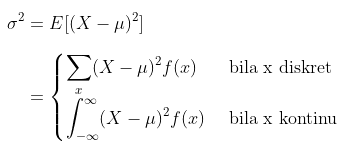
Akar positif variansi, \(σ\), disebut simpangan baku \(X\).
Besaran \(x-μ\) pada definisi di atas disebut penyimpangan suatu pengamatan dari rataannya. Karena penyimpangan ini dikuadratkan dan kemudian dirata-ratakan, maka \(σ^2\) akan lebih kecil untuk suatu kelompok nilai \(x\) yang dekat ke \(μ\) dibandingkan dengan kelompok yang berjauhan dengan \(μ\).
CONTOH 1:
Misalkan peubah acak \(X\) menyatakan banyaknya mobil yang digunakan untuk keperluan dinas kantor pada setiap hari kerja. Distribusi peluang untuk kantor A (Gambar 1a) adalah
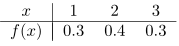
Dan untuk kantor B (Gambar 1b) adalah

Tunjukan bahwa variansi distribusi peluang kantor B lebih besar dari pada variansi kantor A.
Penyelesaian:
Untuk kantor A, diperoleh

dan

Untuk kantor B, dipeoleh
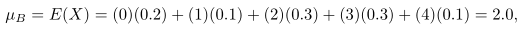
dan

Jelas, varians banyaknya mobil yang digunakan untuk keperluan dinas lebih besar untuk kantor B daripada untuk kantor A.
Rumus mencari varians lain, yang sering lebih mudah, diberikan dalam teorema berikut.
Teorema 1:
Variansi peubah acak \(X\) adalah

Bukti:
Untuk hal diskret dapat ditulis

Karena \( \displaystyle{μ=\sum_x x f(x)} \) menurut definisi dan \( \displaystyle{\sum_x f(x)=1} \) untuk distribusi peluang diskret, maka

Untuk hal kontinu buktinya langkah demi langkah sama, hanya penjumlahan diganti dengan integral.
CONTOH 2:
Misalkan peubah acak \(X\) menyatakan banyaknya bagian yang cacat dari suatu mesin bila 3 suku cadang disampling dari rantai produksi dan diuji. Berikut adalah distribusi peluang \(X\).
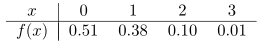
Hitung \(σ^2\) menggunakan Teorema 1.
Penyelesaian:
Pertama-tama, hitung
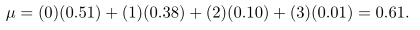
sekarang

Jadi,

CONTOH 3:
Permintaan mingguan Coca Cola, dalam ribuan liter, pada suatu jaringan pemasaran daerah, merupakan peubah acak kontinu \(X\) dengan fungsi padat peluang
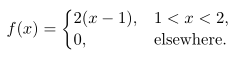
Cari rataan dan variansi \(X\).
Penyelesaian:
Dengan menghitung \(E(X)\) dan \(E(X^2)\), kita peroleh
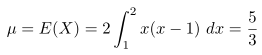
dan

Jadi,

Teorema 2:
Misalkan \(X\) peubah acak dengan distribusi peluang \(f(x)\). Maka variansi peubah acak \(g(X)\) adalah
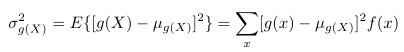
bila \(X\) diskret, dan
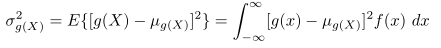
bila \(X\) kontinu.
CONTOH 4:
Hitung variansi \(g(X)=2X+3\), bila \(X\) peubah acak dengan distribusi peluang

Penyelesaian:
Pertama-tama, hitung rataan peubah acak \(2X + 3\) yaitu

Sekarang, gunakan Teorema 2, diperoleh

CONTOH 5:
Misalkan \(X\) peubah acak dengan fungsi padat seperti di Contoh 5 bagian sebelumnya. Cari variansi peubah acak \(g(X)=4X+3\).
Penyelesaian:
Pada Contoh 5 diperoleh \(μ_{(4X+3)}=8\). Sekarang gunakan Teorema 2,
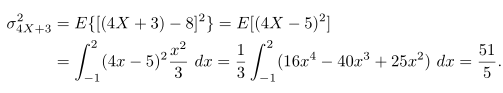
Artikel Terkait
Be not afraid of growing slowly, be afraid only of standing still.
