www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Diskrit › Distribusi Poisson
Peubah Acak Diskrit
Distribusi Poisson
Distribusi Poisson menggambarkan jumlah kejadian diskrit yang terjadi dalam suatu selang waktu atau daerah tertentu. Distribusi Poisson termasuk salah satu distribusi yang penting dan banyak dipergunakan dalam perhitungan-perhitungan statistik.
Distribusi Poisson merupakan salah satu contoh distribusi diskrit yang ditemukan setelah Simon-Denis Poisson (1781-1840), seorang matematika Perancis, mempublikasikannya dalam sebuah paper pada tahun 1837. Distribusi Poisson termasuk salah satu distribusi yang penting dan banyak dipergunakan dalam perhitungan-perhitungan statistik.
Distribusi Poisson menggambarkan jumlah kejadian diskrit yang terjadi dalam suatu selang waktu atau daerah tertentu. Misalnya, berapa jumlah mobil yang tiba secara acak di fasilitas perbaikan mobil selama selang waktu 10 menit.
Contoh lain misalnya, jika \(X\) merupakan suatu peubah acak yang menyatakan jumlah pengunjung dari sebuah toko di antara jam-jam tertentu, maka \(X\) pada umumnya akan memiliki fungsi distribusi Poisson. Banyaknya kecelakaan lalu-lintas yang terjadi setiap hari pada suatu tempat tertentu, pada umumnya juga akan mempunyai penyebaran Poisson.
Definisi:
Distribusi peluang peubah acak Poisson \(X\), yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah tertentu diberikan oleh

di mana \(λ\) menyatakan rata-rata banyaknya sukses yang terjadi per satuan waktu atau daerah tersebut dan \(e=2,71823…\)
Contoh 1:
Rata-rata banyaknya partikel radioaktif yang melewati suatu penghitung selama 1 milidetik dalam suatu percobaan di laboratorium adalah 4. Berapakah peluang 6 partikel melewati penghitung itu dalam 1 milidetik tertentu?
Penyelesaian:
Dengan menggunakan distribusi Poisson untuk \(x = 6\) dan \(λ=4\), dari tabel distribusi Poisson diperoleh
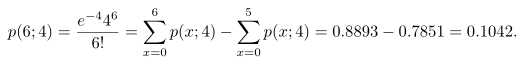
Contoh 2:
Rata-rata banyaknya tanker minyak yang tiba tiap hari di suatu pelabuhan adalah 10. Pelabuhan tersebut hanya mampu menerima paling banyak 15 tanker sehari. Berapakah peluang pada suatu hari tertentu tanker terpaksa ditolak karena pelabuhan tak mampu melayaninya?
Penyelesaian:
Misalkanlah \(X\) menyatakan banyaknya tanker yang tiba tiap hari. Dengan menggunakan tabel distribusi Poisson, diperoleh

Contoh 3:
Dari pengamatan di Terminal Bis Pulo Gadung, ternyata tiap jam terdapat rata-rata 15 bus antar kota datang. Jika banyaknya bis yang datang ini memiliki distribusi Poisson, maka
- Berapa kemungkinannya pada hari sabtu depan antara jam 16.00 – 17.00 terdapat 20 bis datang?
- Pada waktu yang sama, tetapi paling sedikit 10, paling banyak 16?
Penyelesaian:
- Di sini \(λ=15\), jadi
- Untuk bagian (b) yaitu
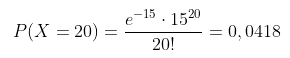
Dengan menggunakan tabel Poisson diperoleh juga 0,0418.

Dengan menggunakan tabel Poisson diperoleh hal yang sama yakni:

Rataan dan Varians Distribusi Poisson
Rataan dan Varians Distribusi Poisson
Rataan dan variansi distribusi Poisson \(p(x;λ)\) keduanya sama dengan \(λ\).
Untuk pembuktian rataan dan varians peubah acak Poisson, klik link berikut: Rataan dan Varians Distribusi Poisson
Fungsi Pembangkit Momen (MGF) Distribusi Poisson
MGF
Fungsi pembangkit momen atau moment generating function (MGF) dari distribusi Poisson yaitu:
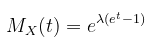
Untuk pembuktian MGF dari distribusi Poisson dan cara mencari nilai harapan \(X\), rataan dan varians menggunakan MGF, klik link berikut. MGF Distribusi Poisson
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
You will face many defeats in life, but never let yourself be defeated.
