Teori Peluang   »   Distribusi Peubah Acak Diskrit   ›  Distribusi Multinomial

Peubah Acak Diskrit

Distribusi Multinomial

Percobaan binomial menghasilkan dua kemungkinan hasil yakni 'sukses' dan 'gagal'. Percobaan binomial akan menjadi percobaan multinomial bila tiap percobaan dapat memberikan lebih dari 2 hasil yang mungkin.

Percobaan binomial yang telah kita bahas sebelumnya merupakan suatu percobaan yang menghasilkan dua kemungkinan hasil yakni 'sukses' dan 'gagal'. Percobaan binomial ini akan menjadi percobaan multinomial bila tiap percobaan dapat memberikan lebih dari 2 hasil yang mungkin.

Dengan demikian, pembagian hasil pabrik menjadi 'ringan', 'berat' atau 'masih dapat diterima' (ada tiga hasil yang mungkin) dan pencatatan kecelakaan di suatu simpang jalan menurut hari dalam seminggu (ada 7 hasil yang mungkin) merupakan contoh percobaan multinomial. Penarikan suatu kartu dari sekotak kartu bridge dengan pengembalian juga merupakan percobaan multinomial bila yang menjadi perhatian adalah keempat warna kartu (4 hasil yang mungkin).

Umumnya, bila suatu percobaan dapat menghasilkan \(k\) hasil yang mungkin \(E_1,E_2,…,E_k\) dengan peluang \(p_1,p_2,…,p_k\) maka distribusi multinomial akan memberikan peluang bahwa \(E_1\) terjadi sebanyak \(x_1\) kali, \(E_2\) sebanyak \(x_2\) kali \(, …, E_k\) sebanyak \(x_k\) kali dalam \(n\) percobaan bebas dengan

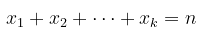
Distribusi peluang gabungan seperti ini akan dinyatakan dengan \(f(x_1,x_2,…,x_k;p_1,p_2,…,p_k,n)\) dengan \(p_1+p_2+⋯+p_k=1\). Perhatikan definisi yang lebih formal berikut ini.

Definisi:

Bila suatu usaha tertentu dapat menghasilkan \(k\) macam hasil \(E_1,E_2,…,E_k\) dengan peluang \(p_1,p_2,…,p_k\) maka distribusi peluang peubah acak \(X_1,X_2,…,X_k\) yang menyatakan banyak terjadinya \(E_1,E_2,…,E_k\) dalam \(n\) usaha bebas ialah

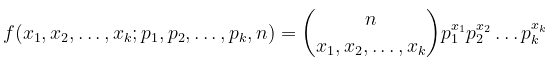
dengan

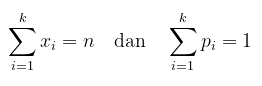
Contoh 1:

Bila dua dadu dilantunkan 6 kali, berapakah peluang mendapat jumlah 7 atau 11 muncul dua kali, sepasang bilangan yang sama satu kali, dan kombinasi lainnya 3 kali?

Pembahasan:

Misalkan \(E_1\) menyatakan jumlah 7 atau 11 muncul, \(E_2\) menyatakan pasangan bilangan yang sama muncul, \(E_3\) menyatakan baik pasangan yang sama maupun jumlah 7 atau 11 tidak muncul.

Peluang masing-masing kejadian di atas ialah \(p_1=2/9, \ p_2=1/6\), dan \(p_3=11/18\). Nilai ini tidak berubah selama keenam usaha dilakukan. Dengan menggunakan distribusi multinomial dengan \(x_1 = 2, \ x_2=1,\ \) dan \(x_3=3\), maka diperoleh peluang yang ditanyakan

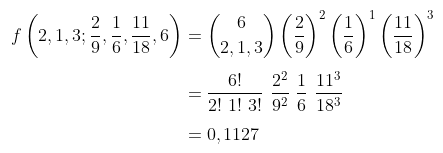
Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.