CONTOH 1:

Berapa banyak titik sampel dalam ruang sampel bila sepasang dadu dilantunkan sekali?

Pembahasan:

Dadu pertama dapat menghasilkan salah satu dari \(n_1=6\) posisi. Untuk tiap posisi tersebut dadu kedua dapat pula menghasilkan \(n_2=6\) posisi. Jadi, pasangan dadu itu dapat menghasilkan \(n_1 n_2=(6)(6)=36\) posisi atau 36 titik sampel.

CONTOH 2:

Suatu perusahaan perumahan menawarkan kepada calon pembeli empat pilihan rumah yaitu rumah dengan gaya luar berbentuk tradisional, Spanyol, kolonial, dan modern di daerah pusat kota, pantai, dan bukit. Berapa banyak pilihan seorang pembeli dapat memesan rumah?

Pembahasan:

Karena \(n_1=4\) dan \(n_2=3\) maka seorang pembeli dapat memilih satu dari \(n_1 n_2 = (4)(3)=12\) kemungkinan rumah.

CONTOH 3:

Berapa macam hidangan dapat disajikan bila masing-masing hidangan dapat terdiri atas sop, nasi goreng, bakmi, dan soto, bila tersedia 4 macam sop, 3 macam nasi goreng, 5 macam bakmi, dan 4 macam soto?

Pembahasan:

Karena \(n_1=4,n_2=3,n_3=5\),dan \(n_4=4\), maka terdapat

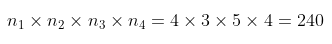
cara berbeda dalam memilih hidangan.

CONTOH 4:

Berapa banyak bilangan genap yang terdiri atas tiga angka dapat dibuat dari angka 1,2,5,6, dan 9 bila tiap angka itu hanya boleh digunakan sekali?

Pembahasan:

Karena bilangan itu genap maka hanya tersedia pilihan \(n_1=2\) untuk satuan (angka terakhir). Untuk tiap satuan ini terdapat \(n_2=4\) pilihan untuk puluhan dan \(n_3=3\) untuk ratusan. Jadi, kita dapat membentuk sebanyak \(n_1 n_2 n_3=(2)(4)(3)=24\) bilangan genap berangka tiga.