Teori Peluang   »   Pembuktian Rataan dan Varians   ›  Rataan dan Varians Distribusi Normal

Distribusi Peubah Acak

Rataan dan Varians Distribusi Normal

Distribusi Normal mengambil peranan penting dalam dunia statistika. Rataan suatu peubah acak yang berdistribusi normal adalah \(μ\), sedangkan variansnya \(σ^2\).

Distribusi Normal mengambil peranan penting dalam dunia statistika. Grafiknya disebut kurva normal, berbentuk lonceng, yang menggambarkan dengan cukup baik berbagai gejala yang muncul di alam, industri, dan penelitian.

Fungsi kepadatan peluang peubah acak normal \(X\), dengan rataan \(μ\) dan varians \(σ^2\), ialah

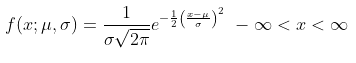
di mana \(π=3,14159…\) dan \(e=2,71828…\)

Bukti: Rataan

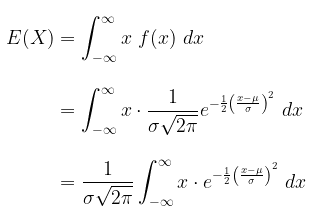
Misalkan \( t=\frac{x-μ}{σ} \), maka \( x = σt + μ \) dan \( dx = σ \ dt \), sehingga

Misalkan lagi: \( z=\frac{1}{2}t^2 \), maka \(dz=t \ dt\), sehingga

Bukti: Varians

Untuk membuktikan varians, kita perlu menentukan nilai harapan \(X^2\) terlebih dahulu.

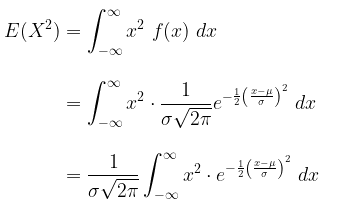
Misalkan \( t=\frac{x-μ}{σ} \), maka \( x = σt + μ \) dan \( dx = σ \ dt \), sehingga

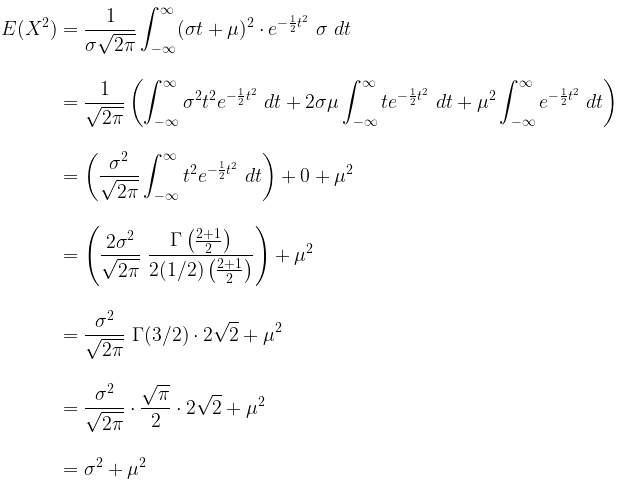
Dengan demikian, variansnya adalah

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.