
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Limit dan Kekontinuan › 30 Contoh Soal dan Pembahasan Limit Trigonometri
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
A PHP Error was encountered
Severity: Notice
Message: Undefined variable: topik
Filename: limit/contoh_soal_dan_pembahasan_limit_trigonometri.php
Line Number: 34
Backtrace:
File: /home/u711839638/domains/jagostat.com/public_html/application/views/matematika_dasar/limit/contoh_soal_dan_pembahasan_limit_trigonometri.php
Line: 34
Function: _error_handler
File: /home/u711839638/domains/jagostat.com/public_html/application/controllers/Matematika_dasar.php
Line: 361
Function: view
File: /home/u711839638/domains/jagostat.com/public_html/index.php
Line: 315
Function: require_once
A PHP Error was encountered
Severity: Notice
Message: Undefined variable: topik
Filename: limit/contoh_soal_dan_pembahasan_limit_trigonometri.php
Line Number: 34
Backtrace:
File: /home/u711839638/domains/jagostat.com/public_html/application/views/matematika_dasar/limit/contoh_soal_dan_pembahasan_limit_trigonometri.php
Line: 34
Function: _error_handler
File: /home/u711839638/domains/jagostat.com/public_html/application/controllers/Matematika_dasar.php
Line: 361
Function: view
File: /home/u711839638/domains/jagostat.com/public_html/index.php
Line: 315
Function: require_once
30 Contoh Soal dan Pembahasan Limit Trigonometri
Ada yang mengatakan bahwa soal limit fungsi trigonometri adalah yang paling sulit di antara soal limit lainnya. Ini karena banyak rumus dan teorema yang mesti dikuasai untuk dapat mengerjakan soal limit fungsi trigonometri dengan lancar. Di artikel ini kita mengulas 30 contoh soal limit fungsi trigonometri dan pembahasannya super lengkap. Ke-30 contoh soal tersebut, yakni:

Sebelum ke pembahasan dari soal-soal tersebut, penting bagi Anda untuk memahami teorema terkait limit fungsi trigonometri berikut ini. Kita akan sering menggunakan teorema ini untuk menyelesaikan soal-soal limit trigonometri.


Contoh Soal dan Pembahasan
Telah kita pelajari bahwa ada beberapa metode atau cara untuk menyelesaikan limit secara umum, antara lain metode substitusi langsung, metode pemfaktoran, metode perkalian akar sekawan, dan lainnya. Beberapa metode itu juga dapat diterapkan untuk menyelesaikan limit fungsi trigonometri.
Soal Nomor 1
Nilai \( \displaystyle \lim_{\theta \to \frac{\pi}{4}} \ \theta \ \tan \theta = \cdots \)
Pembahasan:
Langkah pertama yang biasa dilakukan untuk mencari nilai limit adalah dengan substitusi nilai variabel ke fungsi limitnya. Dalam hal ini, jika kita substitusi \( \theta = \frac{\pi}{4} \) ke fungsi limitnya diperoleh hasil berikut:
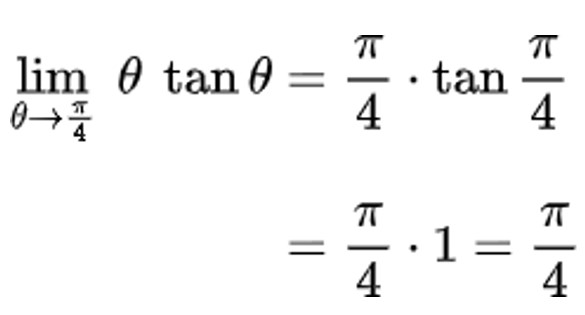
Jadi, nilai dari \( \displaystyle \lim_{\theta \to \frac{\pi}{4}} \ \theta \ \tan \theta = \frac{\pi}{4} \).
Soal Nomor 2
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{1 - \cos x}{x} = \cdots \)
Pembahasan:
Jika kita substitusi nilai \(x = 0\) ke fungsi limitnya diperoleh bentuk tak tentu 0/0 sehingga di sini kita tidak bisa gunakan cara substitusi langsung untuk memperoleh nilai limit.
Kita bisa selesaikan limit tersebut dengan mengalikan pembilang dan penyebut dari fungsi limitnya dengan \((1 + \cos x)\) dan kemudian menggunakan teorema limit trigonometri. Perhatikan berikut ini:
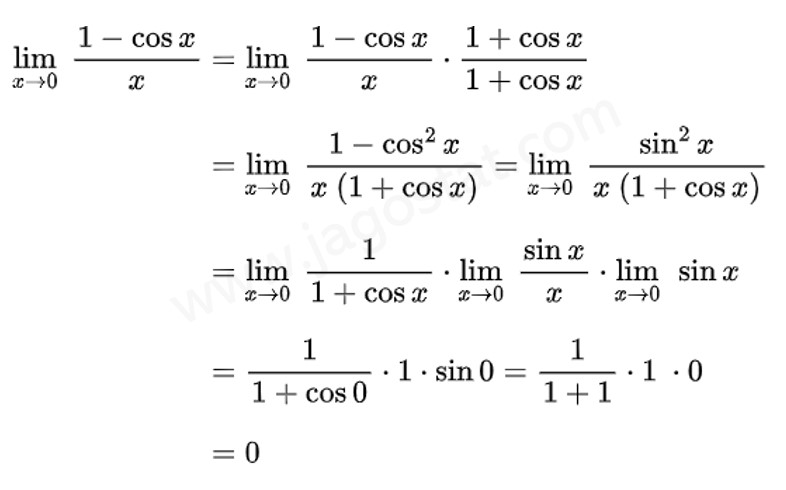
Soal Nomor 3
Nilai \( \displaystyle \lim_{t \to 0} \ \frac{1 - \cos t}{\sin t} = \cdots \)
Pembahasan:
Jika kita substitusi nilai \(t = 0\) ke fungsi limitnya diperoleh bentuk tak tentu 0/0 sehingga di sini kita tidak bisa gunakan cara substitusi langsung untuk memperoleh nilai limit.
Kita bisa selesaikan limit tersebut dengan membagi pembilang dan penyebut dari fungsi limitnya dengan \(t\) dan kemudian menggunakan teorema limit trigonometri. Perhatikan berikut ini:

Jadi, nilai dari \( \displaystyle \lim_{t \to 0} \ \frac{1 - \cos t}{\sin t} = 0 \).
Soal Nomor 4
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{1-\cos 2x}{1-\cos x} = \cdots \)
Pembahasan:
Sama seperti pada Soal 2 dan 3, jika kita substitusi \(x = 0\) ke fungsi limitnya diperoleh bentuk tak tentu 0/0 sehingga kita tidak bisa gunakan cara substitusi langsung untuk menyelesaikan limit ini.
Untuk dapat menyelesaikan limit tersebut, Anda perlu menggunakan rumus identitas trigonometri berikut:

Dengan menggunakan rumus identitas trigonometri di atas, penyelesaian limit dalam soal ini, yaitu:
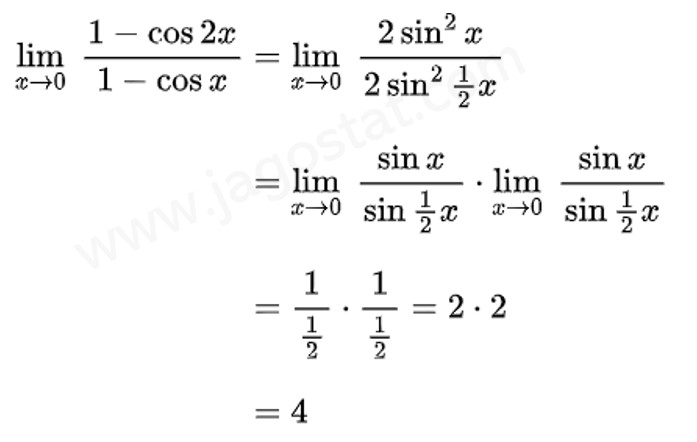
Catatan: Untuk menyelesaikan soal limit trigonometri, biasanya Anda akan sering menggunakan rumus identitas trigonometri untuk mengubah fungsi dalam limitnya sehingga nilai limit tersebut dapat diperoleh. Berikut ini diberikan sejumlah rumus identitas trigonometri yang berguna:

Baca juga:
Untuk soal-soal berikutnya di bawah ini jika kita substitusi nilai variabel ke fungsi limitnya akan diperoleh bentuk tak tentu 0/0 atau \( \infty/\infty \). Dan kita juga akan membuat pembahasannya menjadi lebih ringkas tanpa banyak kata-kata. Intinya, pengerjaannya mirip dengan penjelasan yang diberikan pada beberapa soal di atas.
Soal Nomor 5
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{\sec x - 1}{x} = \cdots \)
Pembahasan:
Ingat: \( \sec x = \frac{1}{\cos x} \) dan \( \displaystyle \lim_{x\to 0} \ \frac{1-\cos x}{x} = 0 \) (Lihat Soal 2).
Dengan demikian, penyelesaian dari limit ini, yaitu:

Soal Nomor 6
Nilai \( \displaystyle \lim_{x \to 0} \ \frac{\cos x - 1}{\sin x} = \cdots \)
Pembahasan:

Soal Nomor 7
Nilai \( \displaystyle \lim_{x \to 0} \ \frac{1-\cos 2x}{2x \sin 2x} = \cdots \)
Pembahasan:

Soal Nomor 8
Nilai \( \displaystyle \lim_{x \to 0} \ \frac{3x \tan 2x}{1 - \cos 4x} = \cdots \)
Pembahasan:

Soal Nomor 9
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{1-\cos 2x}{x \tan 2x} = \cdots \)
Pembahasan:

Soal Nomor 10
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{2 - 2 \cos 2x}{x^2} = \cdots \)
Pembahasan:

Soal Nomor 11
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{\cos 4x - 1}{x \tan 2x} = \cdots \)
Pembahasan:

Soal Nomor 12
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{\tan x - \sin x}{x^3} = \cdots \)
Pembahasan:

Baca juga:
Soal Nomor 13
Nilai \( \displaystyle \lim_{\theta \to \frac{\pi}{2}} \ \frac{\cos^2 \theta}{1 - \sin \theta} = \cdots \)
Pembahasan:
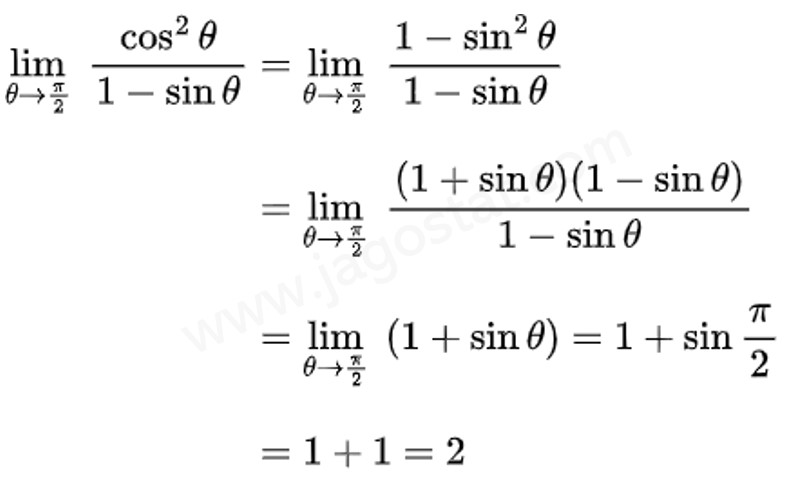
Soal Nomor 14
Nilai \( \displaystyle \lim_{x \to \frac{\pi}{4}} \ \frac{1 - \tan x}{\sin x - \cos x} = \cdots \)
Pembahasan:
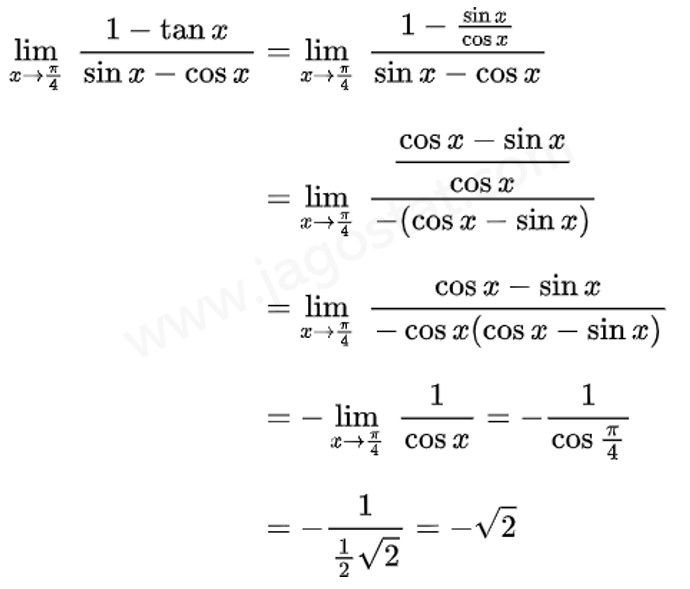
Soal Nomor 15
Nilai \( \displaystyle \lim_{x \to 0} \ \frac{1-\sqrt{\cos x}}{x^2} = \cdots \)
Pembahasan:

Soal Nomor 16
Nilai \( \displaystyle \lim_{x \to \frac{\pi}{8}} \ \frac{\sin^2 2x - \cos^2 2x}{\sin 2x - \cos 2x} = \cdots \)
Pembahasan:

Soal Nomor 17
Nilai \( \displaystyle \lim_{\theta \to 0} \ \frac{1-\cos m\theta}{1-\cos n\theta} = \cdots \)
Pembahasan:

Soal Nomor 18
Nilai \( \displaystyle \lim_{x \to a} \ \frac{\sin (x-a)}{x^2-a^2} = \cdots \)
Pembahasan:
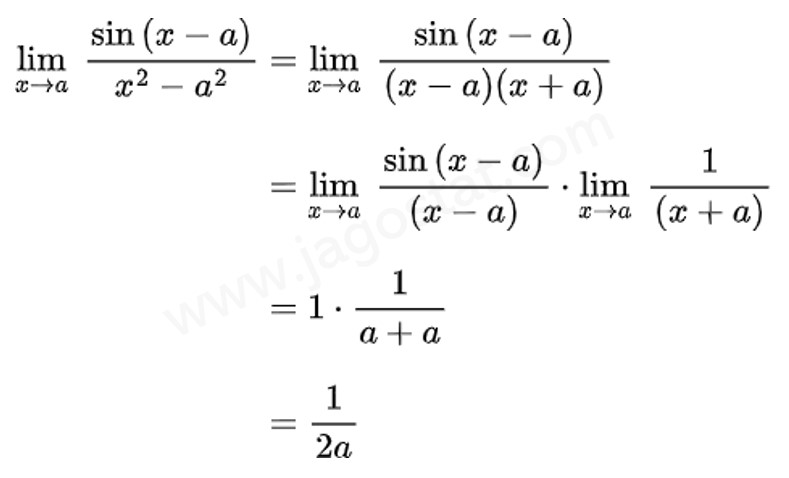
Soal Nomor 19
Nilai \( \displaystyle \lim_{x\to 1} \ \frac{\sin \left( 1 - \frac{1}{x} \right) \cos \left( 1 - \frac{1}{x} \right)}{x-1} = \cdots \)
Pembahasan:

Baca juga:
Soal Nomor 20
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{\cos 3x - \cos x}{x^2} = \cdots \)
Pembahasan:

Soal Nomor 21
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{\sin 5x - \sin 3x}{\sin x} = \cdots \)
Pembahasan:
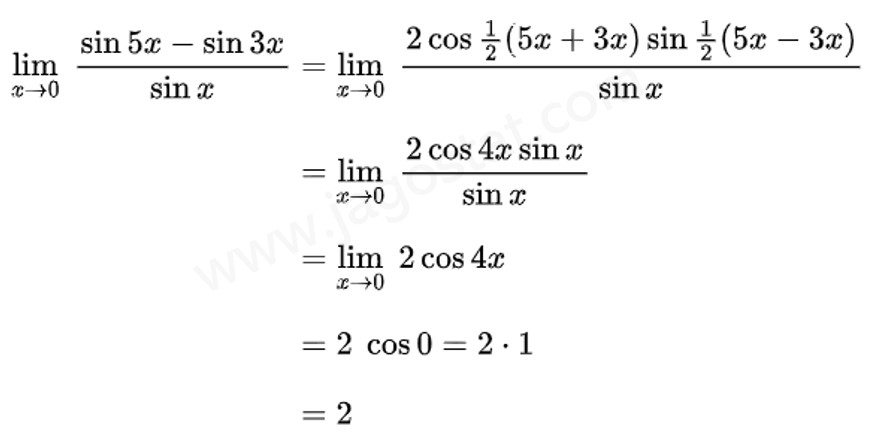
Soal Nomor 22
Nilai \( \displaystyle \lim_{x\to 0} \ \frac{\cos (x+a) - \cos (x-a)}{x} = \cdots \)
Pembahasan:
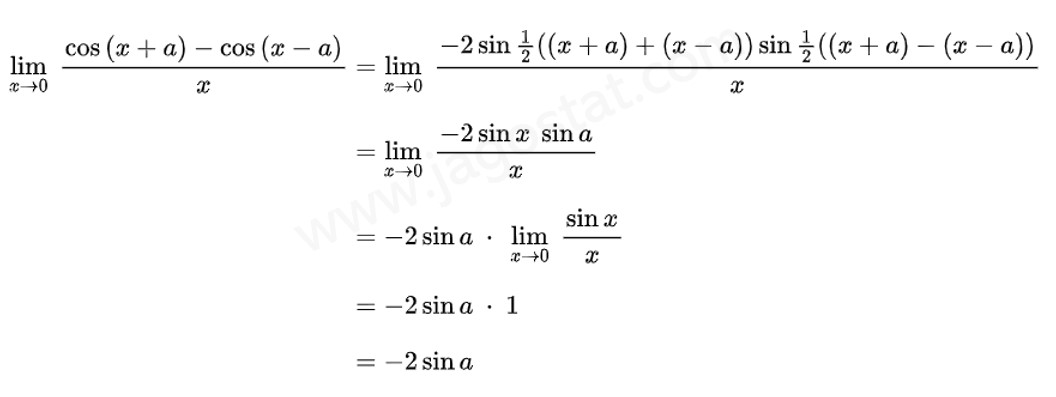
Soal Nomor 23
Nilai \( \displaystyle \lim_{x\to b} \ \frac{\sin x - \sin b}{x - b} = \cdots \)
Pembahasan:

Soal Nomor 24
Nilai \( \displaystyle \lim_{x \to \theta} \ \frac{x \sin \theta - \theta \sin x}{x-\theta} = \cdots \)
Pembahasan:
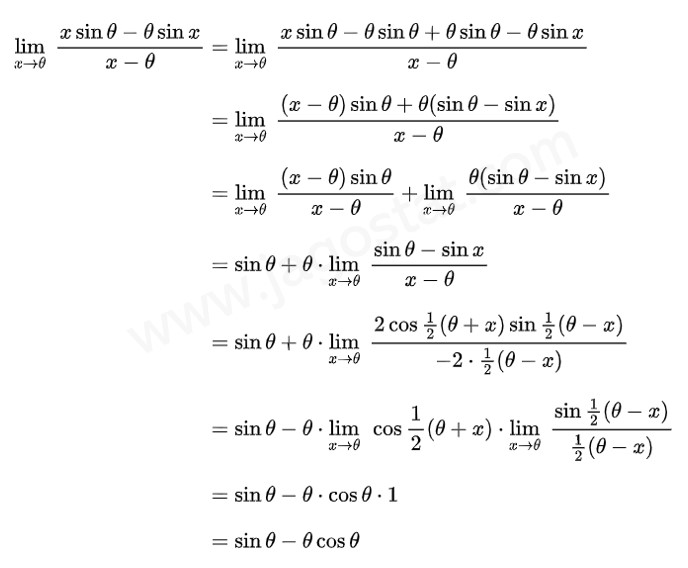
Soal Nomor 25
Nilai \( \displaystyle \lim_{x \to 0} \ \frac{\sin (\pi x-\pi)}{(x-1) \cos (\pi x-\pi)} = \cdots \)
Pembahasan:

Soal Nomor 26
Nilai \( \displaystyle \lim_{x \to 0} \ \frac{\sin (x-1)}{x^2+x-2} = \cdots \)
Pembahasan:

Soal Nomor 27
Nilai \( \displaystyle \lim_{x \to \frac{\pi}{4}} \ \frac{\cos 2x}{\sin x - \cos x} = \cdots \)
Pembahasan:

Soal Nomor 28
Nilai \( \displaystyle \lim_{x \to 1} \ \frac{(x^2-1)\tan (2x-2)}{\sin^2 (x-1)} = \cdots \)
Pembahasan:
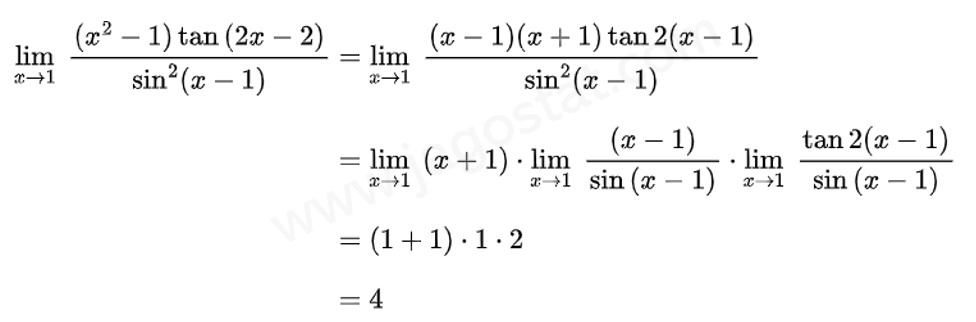
Soal Nomor 29
Nilai \( \displaystyle \lim_{x\to 0} \ \left( \frac{\sin 4x}{x^2 \tan 2x} - \frac{2}{x^2} \right) = \cdots \)
Pembahasan:

Soal Nomor 30
Nilai \( \displaystyle \lim_{x\to 2} \ \frac{(x-2) \cos (\pi x- 2 \pi)}{\tan (2\pi x - 4 \pi)} = \cdots \)
Pembahasan:

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Spend more time smiling than frowning and more time praising than criticizing.