
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Persamaan Polinomial › Mencari Akar-akar Persamaan Kuadrat dengan Pemfaktoran
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Mencari Akar-akar Persamaan Kuadrat dengan Pemfaktoran
Pada umumnya, terdapat tiga cara untuk mencari akar-akar suatu persamaan kuadrat, yaitu cara pemfaktoran, melengkapkan kuadrat sempurna, dan rumus abc.
Persamaan kuadrat atau persamaan polinomial (suku banyak) dengan pangkat tertinggi dua dapat dituliskan sebagai

dengan \(a, b\), dan \(c\) merupakan bilangan real dan \(a≠0\).
Solusi penyelesaian suatu persamaan kuadrat disebut sebagai akar-akar persamaan kuadrat tersebut. Yang dimaksud dengan akar-akar persamaan kuadrat adalah nilai dari variabel \(x\) yang memenuhi ketika disubstitusikan ke dalam persamaan kuadrat tersebut.
Pada umumnya terdapat tiga cara untuk mencari akar-akar persamaan kuadrat, yaitu cara pemfaktoran, melengkapkan kuadrat sempurna, dan rumus abc. Pada artikel ini kita akan bahas cara pemfaktoran.
Dalam mencari akar persamaan kuadrat dengan pemfaktoran, kita membuat persamaan kuadrat tersebut menjadi perkalian dua persamaan linear. Perhatikan contoh persamaan kuadrat beserta hasil pemfaktorannya berikut ini:

Perhatikan bahwa ada empat bentuk persamaan kuadrat dan hasil pemfaktorannya pada contoh di atas. Keempat bentuk persamaan kuadrat tersebut dapat dinyatakan sebagai
- Persamaan kuadrat bentuk \(ax^2+bx+c=0\) dengan \(a = 1\)
- Persamaan kuadrat bentuk \(ax^2+bx+c=0\) dengan \(a≠1\) dan \(a≠0\)
- Persamaan kuadrat bentuk \(ax^2+bx=0\) dengan \(c=0\)
- Persamaan kuadrat bentuk \(x^2-4=0\) dengan \(b=0\)
Hal yang perlu dicatat ialah bahwa terdapat perlakuan yang sedikit berbeda dalam memfaktorkan atau mencari akar-akar persamaan kuadrat untuk masing-masing kasus di atas. Kita akan membahas satu demi satu cara memfaktorkan keempat bentuk persamaan tersebut.
Baca juga:
Mencari Akar Persamaan Kuadrat Bentuk \(ax^2+bx+c=0\) dengan \(a = 1\).
Untuk mencari akar-akar persamaan kuadrat bentuk ini dengan cara pemfaktoran, perhatikanlah tabel yang membantu berikut ini.

Beberapa langkah yang perlu dilakukan yaitu:
- Tentukanlah dua angka sembarang, misalnya \(p\) dan \(q\), yang mana jika dijumlahkan hasilnya sama dengan \(b \ (p + q = b)\) dan jika dikalikan hasilnya sama dengan \(ac \ (p × q = ac)\) dan karena \(a = 1\), maka \(p × q = c\). Untuk menentukan pasangan angka \(p\) dan \(q\), kita dapat mencari bilangan-bilangan yang merupakan faktor dari \(ac\) atau \(c\) saja karena \(a = 1\).
- Setelah nilai \(p\) dan \(q\) telah ditentukan, substitusikan nilai \(p\) dan \(q\) tersebut pada rumus pemfaktoran yang diberikan pada tabel di atas.
Untuk lebih memahami penjelasan di atas, perhatikanlah contoh berikut:
Contoh 1:
Dengan cara pemfaktoran, tentukanlah akar-akar dari persamaan berikut.
- \( x^2-5x+6 = 0 \)
- \( x^2 + 9x + 14 = 0 \)
Pembahasan:
- Perhatikan bahwa untuk \(x^2-5x+6=0\), maka \(a = 1, \ b = -5, \ c = 6\) dan \(ac = 1 × 6 = 6\). Untuk menentukan nilai \(p\) dan \(q\) kita cari terlebih dahulu faktor dari 6 yakni
- Untuk persamaan kuadrat \(x^2+9x+14=0\), maka \(a = 1, \ b = 9, \ c = 14\) dan \(ac = 1 × 14 = 14\). Faktor dari 14 yaitu

Dari delapan angka di atas, tentukanlah dua angka yang jika dijumlahkan hasilnya sama dengan -5 dan jika dikalikan hasilnya sama dengan 6. Angka yang memenuhi kondisi tersebut yaitu -2 dan -3. Jadi, kita peroleh \(p = - 2\) dan \(q = -3\) (atau kebalikannya). Dengan substitusi nilai \(p\) dan \(q\) ke rumus pemfaktoran, kita peroleh

Dengan demikian, akar-akar dari persamaan kuadrat \(x^2-5x+6=0\) adalah \(x_1 = 2\) dan \(x_2 = 3\).

Dari delapan angka di atas, tentukanlah dua angka yang jika dijumlahkan hasilnya sama dengan 9 dan jika dikalikan hasilnya sama dengan 14. Dua angka tersebut yaitu 2 dan 7. Jadi, kita peroleh \(p = 2\) dan \(q = 7\). Dengan substitusi nilai \(p\) dan \(q\) ke rumus pemfaktoran, kita peroleh
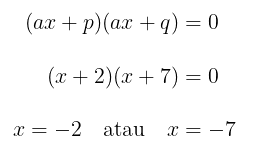
Dengan demikian, akar-akar dari persamaan kuadrat \(x^2+9x+14=0\) adalah \(x_1 = -2\) dan \(x_2 = -7\).
Akar Persamaan Kuadrat Bentuk \(ax^2+bx+c = 0\) dengan \(a≠1\)
Untuk menentukan akar-akar persamaan kuadrat bentuk ini, perhatikan tabel yang membantu berikut ini.

Langkah-langkah untuk menemukan akar-akar persamaan kuadrat bentuk ini mirip dengan yang sudah kita bahas di atas yaitu pertama carilah nilai \(p\) dan \(q\) di mana jika dijumlahkan hasilnya sama dengan b dan jika dikalikan hasilnya sama dengan ac. Setelah nilai \(p\) dan \(q\) telah ditentukan, substitusikan nilai \(p\) dan \(q\) tersebut pada rumus pemfaktoran yang diberikan pada tabel di atas. Perhatikanlah contoh berikut ini.
Contoh 2:
Dengan cara pemfaktoran, tentukanlah akar-akar dari persamaan berikut.
- \( 2x^2-4x-16=0 \)
- \( 4x^2-16x+15 = 0 \)
Pembahasan:
- Untuk persamaan kuadrat \(2x^2-4x-16=0\), maka \(a = 2, \ b = -4, \ c = -16\), dan \(ac = 2 × -6 = - 32\). Untuk menentukan nilai \(p\) dan \(q\) kita cari dulu faktor dari -32 yaitu
- Untuk persamaan kuadrat \(4x^2-16x+15 = 0\), maka \(a = 4, \ b = -16, \ c = 15\), dan \(ac = 4 × 15 = 60\). Untuk menentukan nilai \(p\) dan \(q\) kita cari dulu faktor dari 60 yaitu

Dari angka-angka di atas, pasangan angka yang jika dijumlahkan hasilnya -4 dan jika dikalikan hasilnya -32 adalah 4 dan -8. Jadi, kita peroleh \(p = 4\) dan \(q = -8\). Dengan substitusi nilai \(p\) dan \(q\) ke rumus pemfaktoran, kita peroleh

Dengan demikian, akar-akar dari \(2x^2-4x-16=0\) adalah \(x_1 = 4\) dan \(x_2 = -2\).

Dari angka-angka di atas, pasangan angka yang jika dijumlahkan hasilnya -16 dan jika dikalikan hasilnya 60 adalah -6 dan -10. Jadi, kita peroleh \(p = -6\) dan \(q = -10\). Dengan substitusi nilai \(p\) dan \(q\) ke rumus pemfaktoran, kita peroleh

Dengan demikian, akar-akar dari \(4x^2-16x+15 = 0\) adalah \(x_1 = 3/2\) dan \(x_2 = 5/2\).
Baca juga:
Akar Persamaan Kuadrat Bentuk \(ax^2+bx=0\)
Untuk menentukan akar-akar persamaan kuadrat bentuk \(ax^2+bx=0\), kita bisa mengubah bentuk persamaan kuadrat ini menjadi bentuk perkalian faktor-faktor aljabar dalam variabel \(x\). Perhatikan berikut ini.

Dengan demikian, akar-akar persaman kuadrat bentuk \(ax^2+bx=0\) adalah 0 dan \(–b/a\). Perhatikan contoh soal berikut.
Contoh 3:
Dengan cara pemfaktoran, tentukanlah akar-akar dari persamaan berikut.
- \( 4x^2-12x=0 \)
- \( 3x^2+7x=0 \)
Pembahasan:
- Untuk \(4x^2-12x=0\), maka
- Kita dapat menentukan akar persamaan kuadrat \( 3x^2+7x=0 \) dengan cepat yaitu dengan menggunakan ketentuan \(x = 0\) atau \(x = -b/a\) sehingga akar-akar dari persamaan kuadrat ini adalah 0 dan -7/3.

Dengan demikian, akar-akar dari \(4x^2-12x=0\) adalah 0 atau 3.
Akar Persamaan Kuadrat Bentuk \(x^2-c=0\)
Untuk mencari akar-akar persamaan kuadrat bentuk \(x^2-c=0\) kita bisa mengubahnya menjadi bentuk perkalian faktor-faktornya, yakni
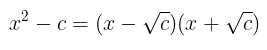
Dengan demikian, kita peroleh akar-akarnya yaitu \(\sqrt{c}\) dan \(-\sqrt{c}\). Perhatikanlah beberapa contoh berikut ini.
Contoh 4:
Tentukan akar-akar persamaan berikut dengan cara pemfaktoran.
- \( x^2 - 9 = 0 \)
- \( x^2 - 36 = 0 \)
Pembahasan:
- Untuk \(x^2-9=0\), maka
- Dengan cara yang sama seperti pada (a), kita peroleh

Dengan demikian, akar-akar dari \(x^2-9=0\) yaitu 3 dan -3.
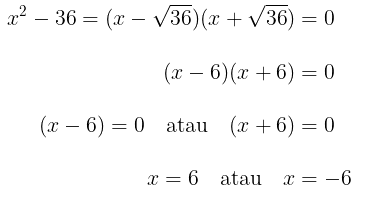
Dengan demikian, akar-akar dari \(x^2-36=0\) yaitu 6 dan -6.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The only way to do great work is to love the work you do.
