www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Bentuk Pangkat, Akar, dan Logaritma › Bentuk Akar dan Sifat-sifatnya
Bentuk Akar dan Sifat-sifatnya
Bentuk akar merupakan bentuk lain untuk menyatakan bilangan berpangkat. Bentuk akar termasuk dalam bilangan irasional, yakni bilangan yang tidak dapat dinyatakan dengan pecahan \(a/b\), di mana \(a\) dan \(b\) bilangan bulat dan \(b ≠ 0\).
Dalam bentuk akar (radikal), terdapat 3 bagian yang perlu diketahui yaitu lambang bentuk akar, radikan, dan indeks. Secara umum, bentuk akar dapat dituliskan sebagai
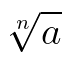
di mana \( \sqrt[n]{a} \) dibaca "akar pangkat n dari a" dan disebut bentuk akar (radikal), \(\sqrt{}\) disebut lambang bentuk akar, n disebut indeks (pangkat akar), dan a disebut radikan (bilangan di dalam akar) dengan a bilangan riil positif untuk n bilangan asli dan a bilangan riil negatif untuk n bilangan ganjil.
Sama seperti bentuk pangkat, bentuk akar juga memiliki beberapa sifat-sifat penting, yakni
- Untuk a, b bilangan riil dan n bilangan asli yang sesuai berlaku
- Untuk sebarang nilai a dengan \( a \neq 0 \), m bilangan bulat, n bilangan asli dan \( n \geq 2 \), berlaku


Contoh 1:
Dengan menggunakan sifat-sifat bentuk akar, sederhanakanlah bentuk akar berikut.

Pembahasan »

Merasionalkan Penyebut Bentuk Akar
Dalam suatu bentuk operasi bilangan, ada kalanya bilangan tersebut memiliki penyebut dalam bentuk akar, seperti:
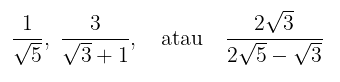
Bentuk-bentuk bilangan tersebut dapat disederhanakan dengan cara merasional penyebut pecahan-pecahan tersebut.
Kegiatan merasionalkan pada intinya mengubah bentuk akar pada penyebut menjadi bentuk bilangan rasional, yang pada akhirnya bilangan tersebut dapat dinyatakan dalam bentuk yang lebih sederhana. Suatu bentuk pecahan yang memuat bilangan bentuk akar dikatakan sederhana jika dipenuhi:
- Setiap bilangan bentuk akarnya sudah dalam bentuk sederhana, dan
- tidak ada bentuk akar pada penyebut jika bilangan tersebut pecahan.
Pada artikel ini, kita akan mempelajari cara merasionalkan berbagai bentuk pecahan agar lebih sederhana.
#1. Pecahan bentuk \( \frac{a}{\sqrt{b}} \)
Bentuk akar \( \frac{a}{\sqrt{b}} \) dengan \( b \neq 0 \) dapat dirasionalkan penyebutnya dengan cara mengalikan pecahan dengan \( \sqrt{b} \) sehingga
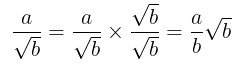
Contoh 3:
Sederhanakanlah penyebut dari bentuk pecahan berikut.
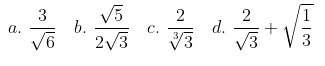
Pembahasan »

c. Agar penyebut \( \sqrt[3]{3} \) dapat dirasionalkan, maka \( \sqrt[3]{3} \) dikalikan dengan \( \sqrt[3]{3^2} \) sehingga didapat penyelesaian sebagai berikut:


#2. Pecahan bentuk \( \frac{a}{b-\sqrt{c}} \)
Untuk menyederhanakan bentuk pecahan \( \frac{a}{b+\sqrt{c}} \) atau \( \frac{a}{b-\sqrt{c}} \), kalikan bentuk pecahan dengan bentuk sekawan dari penyebut. Bentuk sekawan dari \( b + \sqrt{c} \) adalah \( b - \sqrt{c} \). Sebaliknya, bentuk sekawan dari \( b - \sqrt{c} \) adalah \( b + \sqrt{c} \), sehingga

#3. Pecahan bentuk \( \frac{a}{\sqrt{b}-\sqrt{c}} \)
Untuk menyederhanakan penyebut dari bentuk pecahan \( \frac{a}{\sqrt{b}+\sqrt{c}} \) atau \( \frac{a}{\sqrt{b}-\sqrt{c}} \), kalikan pecahan dengan bentuk sekawan dari penyebutnya. Bentuk sekawan dari \( \sqrt{b}+\sqrt{c} \) adalah \( \sqrt{b}-\sqrt{c} \). Sebaliknya, bentuk sekawan dari \( \sqrt{b}-\sqrt{c} \) adalah \( \sqrt{b}+\sqrt{c} \), sehingga

#4. Menyederhanakan bentuk \( \sqrt{(a+b)-2\sqrt{a⋅b}} \)
Bentuk \( \sqrt{(a+b)-2\sqrt{a⋅b}} \) dapat diubah menjadi bentuk \( \sqrt{a} \pm \sqrt{b} \) dengan syarat \(a, b \in R\) dan \(a > b\).
Bukti:

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The best and most beautiful things in this world cannot be seen or even heard, but must be felt with the heart.