
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Turunan › Contoh Soal dan Pembahasan Turunan Fungsi Trigonometri Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Contoh Soal dan Pembahasan Turunan Fungsi Trigonometri Matematika SMA
Pada artikel ini kita akan membahas beberapa contoh soal turunan fungsi trigonometri matematika SMA. Pada dasarnya, menyelesaikan soal turunan fungsi trigonometri mirip dengan cara menyelesaikan turunan fungsi aljabar yakni kita dapat menggunakan rumus-rumus turunan seperti turunan perkalian, pembagian, dan turunan fungsi komposisi dengan aturan rantai.
Hanya saja, karena di sini fungsi yang akan dicari turunannya adalah fungsi trigonometri maka kita perlu pahami dulu turunan dari fungsi trigonometri dasar berikut ini:

Perhatikan bahwa kita menggunakan notasi \( f’(x) \) untuk menyatakan turunan seperti diberikan di atas. Sebenarnya masih ada beberapa cara lain untuk menyatakan turunan, yakni:
\[ y' \quad \frac{dy}{dx} \quad \text{dan} \quad Dx \]
Sebelum masuk ke contoh soal dan pembahasan dari turunan fungsi trigonometri, sebaiknya kita sudah menguasai beberapa rumus turunan berikut ini agar dapat mengerjakan soal turunan trigonometri dengan lancar.

Untuk lebih jelasnya, kita langsung masuk ke contoh soal dan pembahasan turunan fungsi trigonometri berikut ini.
Contoh 1:
Jika \( f(x)=-(\cos^2 x - \sin^2 x) \), maka \( f’(x) \) adalah…
Pembahasan »Untuk mengerjakan soal ini kita bisa meminjam sifat dari identitas trigonometri berikut:
\begin{aligned} \sin 2x &= 2 \sin x \cos x \\[8pt] \cos 2x &= \cos^2 x - \sin^2 x \end{aligned}
Dengan demikian,

Contoh 2:
Jika \( y = 3x^4 + \sin 2x + \cos 3x \), maka \( \displaystyle \frac{dy}{dx} = \cdots \)
Pembahasan »
Contoh 3:
Jika \( y = 2 \sin 3x – 3 \cos 2x \), maka \( \displaystyle \frac{dy}{dx} = \cdots \)
Pembahasan »
Contoh 4:
Jika \( \displaystyle f(x) = \frac{ \sin x + \cos x }{ \sin x }, \sin x \neq 0 \) dan \( f’(x) \) adalah turunan \( f(x)\), maka \( \displaystyle f’ \left( \frac{\pi}{2} \right) = \cdots \)
Pembahasan »Misalkan: \( u = \sin x + \cos x \) dan \( v = \sin x \) sehingga \( f(x) = u/v \). Ingat bahwa rumus turunan untuk pembagian yaitu:
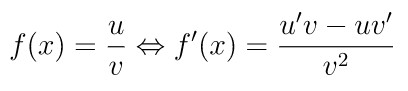
Kita cari turunan dari \(u\) dan \(v\) terlebih dahulu, yakni:

Dengan demikian,

Baca juga:
Contoh 5:
Jika \( \displaystyle f(x) = a \tan x + bx, \ f’ \left( \frac{\pi}{4} \right) = 3 \) dan \( \displaystyle f’ \left( \frac{\pi}{3} \right) = 9 \), maka \( a + b = \cdots \)
Pembahasan »Ingat bahwa turunan dari \( \tan x \) adalah \( \sec^2 x \) sehingga

Selanjutnya, dengan menyelesaikan SPLDV (persamaan 1 dan 2) di atas dengan cara substitusi atau eliminasi, kita peroleh nilai \(a = 3\) dan \(b = -3\) sehingga \(a + b = 0\).
Contoh 6:
Turunan pertama dari \( y = \cos^4 x \) adalah…
Pembahasan »Untuk menyelesaikan soal turunan ini kita bisa gunakan aturan rantai. Misalkan \( u = \cos x \) sehingga kita dapatkan hasil berikut:

Dengan demikian, turunan pertama dari \( y = \cos^4 x \) dengan cara aturan rantai, yakni:

Contoh 7:
Jika \( f(x) = \sin (\sin^2 x) \), maka \( f’(x) = \cdots \)
Pembahasan »Untuk mencari turunan pertama dari fungsi pada soal di atas, kita bisa gunakan aturan rantai. Misalkan \( u = \sin x \) sehingga

Misalkan lagi \( v = u^2 \) sehingga

Dengan demikian, turunan pertama dari \( f(x) = \sin (\sin^2 x) \) berdasarkan aturan rantai, yaitu:

Contoh 8:
Misalkan \( f(x) = 2 \tan (\sqrt{\sec x}) \), maka \( f’(x) = \cdots \)
Pembahasan »Kita dapat gunakan aturan rantai untuk menyelesaikan soal ini. Misalkan \( u = \sec x \) sehingga

Misalkan lagi \( v = \sqrt{u} \) sehingga
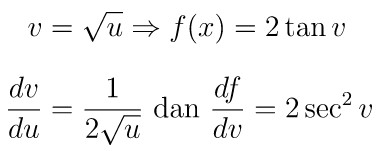
Dengan demikian, turunan pertama dari \( f(x) = \sin (\sin^2 x) \) berdasarkan aturan rantai, yaitu:
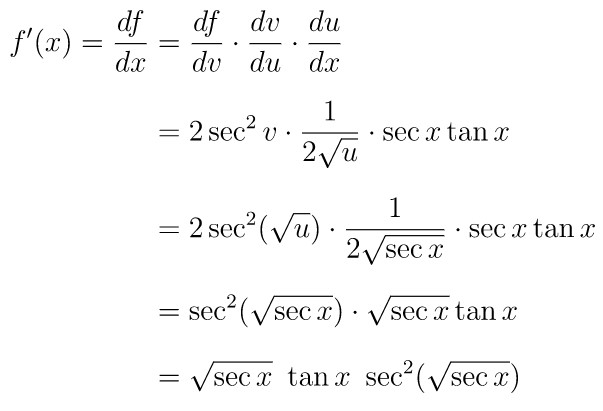
Contoh 9:
Turunan pertama dari fungsi \( \displaystyle f(x) = \frac{1+\cos x}{\sin x} \) adalah \( f’(x) = \cdots \)
Pembahasan »Misalkan: \( u = 1 + \cos x \) dan \( v = \sin x \) sehingga \( f(x) = u/v \). Ingat bahwa rumus turunan untuk pembagian yaitu:

Kita cari turunan dari \(u\) dan \(v\) terlebih dahulu, yakni:

Dengan demikian,

Baca juga:
Contoh 10:
Jika fungsi \( f(x) = \sin ax + \cos bx \) memenuhi \( f’(0) = b \) dan \( \displaystyle f’ \left( \frac{\pi}{2a} \right) = -1 \), maka \(a + b = \cdots \)
Pembahasan »

Karena \( b = a \) dan \(a = 1\), maka \(b\) juga bernilai 1 sehingga \( a + b = 1 + 1 = 2 \).
Contoh 11:
Jika \( f(x) = \sin x \cos 3x \), maka \( \displaystyle f’ \left( \frac{1}{6} \pi \right) = \cdots \)
Pembahasan »Misalkan \( u = \sin x \) dan \( v = \cos 3x \) sehingga \( f(x) = u \cdot v \). Ingat bahwa rumus turunan dari perkalian dua fungsi yaitu:

Selanjutnya, kita cari turunan dari u dan v terlebih dahulu, yakni:

Dengan demikian,

Contoh 12:
Turunan pertama dari fungsi \( y = (\sin x + \cos x)^2 \) adalah…
Pembahasan »Untuk mencari turunan dari fungsi dalam soal ini ada dua cara yang bisa digunakan. Cara yang pertama yaitu dengan menyederhanakan fungsinya terlebih dahulu lalu mencari turunannya. Perhatikan berikut ini:
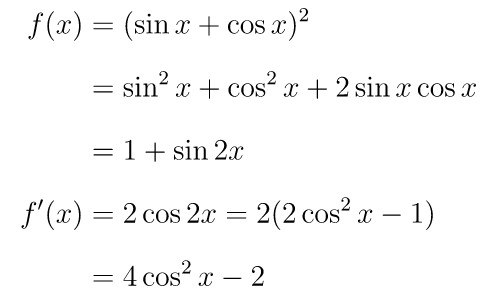
Cara kedua yaitu langsung menggunakan sifat dari turunan.
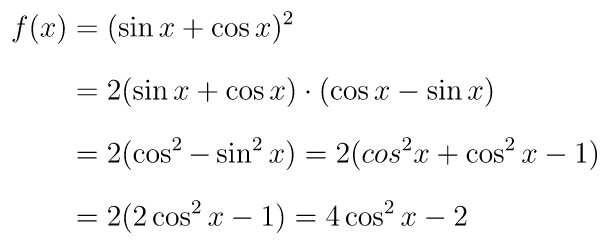
Contoh 13:
Jika \( f(x) = \sqrt{1+\sin^2 x} \) di mana \( 0 \leq x \leq \pi \), maka \( f’(x) \cdot f(x) \) sama dengan…
Pembahasan »
Contoh 14:
Diketahui \( f(x) = x \sin 3x \), maka \( f’ \left( \frac{\pi}{4} \right) \) sama dengan…
Pembahasan »Misalkan \( u = x \) dan \( v = \sin 3x \), maka \( f(x) = u \cdot v \). Ingat bahwa rumus turunan dari perkalian dua fungsi, yaitu:
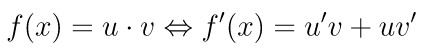
Selanjutnya, kita cari turunan dari \(u\) dan \(v\) terlebih dahulu, yakni:

Dengan demikian, turunan dari \( f(x) = x \sin 3x \), yakni:
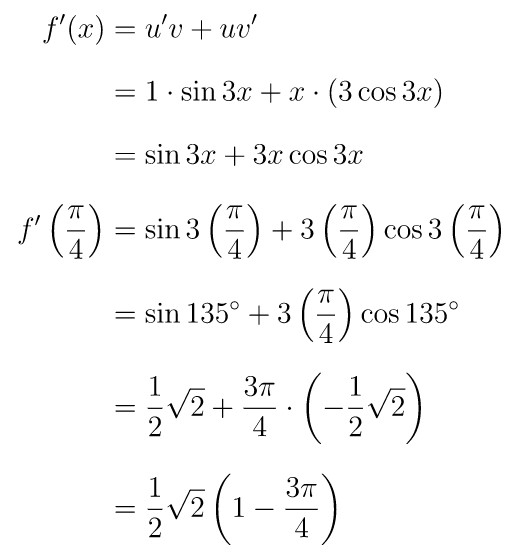
Contoh 15:
Jika \( \displaystyle f(x) = \frac{ \cos x - \sin x }{ \cos x + \sin x } \), dengan \( \cos x + \sin x \neq 0 \), maka \( f’(x) = \cdots \)
Pembahasan »Misalkan \( u = \cos x - \sin x \) dan \( v = \cos x + \sin x \) sehingga \( f(x) = u/v \). Ingat bahwa rumus turunan dari pembagian dua fungsi, yaitu:

Kita cari turunan dari \(u\) dan \(v\) terlebih dahulu, yakni:

Dengan demikian,

Contoh 16:
Jika \( f(x) = x \cos x \), maka \( \displaystyle f’ \left(x + \frac{\pi}{2} \right) = \cdots \)
Pembahasan »Ingat bahwa:


Sekarang kita akan menyelesaikan turunan dari fungsi di atas menggunakan rumus turunan untuk perkalian dua fungsi. Misalkan \( u = - \left( x + \frac{\pi}{2} \right)\) dan \( v = \sin x \) sehingga

Dengan demikian,

Contoh 17:
Jika \( f(x) = (\sin x + \cos x)(\cos 2x + \sin 2x) \) dan \( f’(x) = 2 \cos 3x + g(x) \), maka \( g(x) = \cdots \)
Pembahasan »Untuk menyelesaikan soal ini kita mungkin memerlukan catatan rumus jumlah dan selisih dua sudut pada perbandingan trigonometri.

Jadi, \( g(x) = \cos 3x - \sin x \).
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel terkait
Our greatest weakness lies in giving up. The most certain way to succeed is always to try just one more time.
