
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Limit Fungsi › Aturan L'Hospital untuk Menyelesaikan Limit Tak Tentu
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Aturan L'Hospital untuk Menyelesaikan Limit Tak Tentu
Aturan L’Hospital atau Dalil L’Hospital digunakan untuk menyelesaikan limit yang hasilnya berupa bentuk tak tentu terutama yang berbentuk 0/0 atau ∞/∞.
Aturan L’Hospital atau Dalil L’Hospital digunakan untuk menyelesaikan limit yang hasilnya berupa bentuk tak tentu terutama yang berbentuk 0/0 atau ∞/∞. Perhatikan dua contoh limit berikut:

Pada limit pertama, jika kita substitusi \(x = 5\) ke fungsi dalam limitnya kita peroleh hasil 0/0. Begitu pula, pada limit kedua, jika kita substitusi \(x = ∞\), kita peroleh hasil \(∞/∞\). Kedua hasil yang kita peroleh ini disebut sebagai bentuk tak tentu.

Bagaimana kita menyelesaikan limit yang demikian? Sebenarnya, dalam kasus tertentu kita dapat menyelesaikan limit tersebut dengan cara pemfaktoran jika memang memungkinkan atau dengan metode pembagian pangkat tertinggi. Namun, terdapat cara yang lebih mudah yaitu menggunakan Aturan L'Hospital.
Aturan L’Hospital menggunakan konsep turunan (diferensial) untuk menyelesaikan limit tak tentu. Oleh karena itu, untuk dapat menggunakan Aturan L'Hospital dengan baik teman-teman perlu memahami cara mencari turunan dari suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri.
Definisi: Aturan L'Hospital
Misalkan kita memiliki limit dengan hasil tak tentu berikut:

di mana \(a\) dapat berupa sembarang bilangan riil, tak hingga negatif maupun positif. Menurut Aturan L’Hospital, kita peroleh hasil berikut:
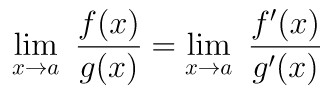
Jadi, Aturan L’Hospital memberitahu kita bahwa jika kita memiliki limit bentuk tak tentu 0/0 atau ∞/∞, maka limit tersebut dapat diselesaikan dengan menurunkan pembilang dan penyebut dari fungsi limitnya, kemudian substitusi nilai \(x\) ke fungsi yang telah diturunkan tersebut untuk memperoleh nilai limit yang diinginkan.
Baca juga:
Untuk mendapatkan pemahaman yang lebih baik mengenai Aturan L’Hospital ini, perhatikan beberapa contoh soal berikut.
Contoh 1:
Hitunglah \( \displaystyle \lim_{x \to 5} \ \frac{x^2-25}{x-5} \).
Pembahasan:
Seperti yang sudah kita singgung di awal, jika kita substitusi nilai \(x = 5\) ke fungsi limitnya kita peroleh bentuk tak tentu 0/0 sehingga kita dapat menerapkan Aturan L'Hospital untuk menyelesaikan limit ini.
Sebenarnya, kita dapat menyelesaikan limit ini dengan cara pemfaktoran, yakni:

Namun, kita tidak selalu dapat menggunakan cara pemfaktoran. Jika demikian halnya, kita dapat menggunakan Aturan L'Hospital. Perhatikan bahwa pembilang dari fungsi limitnya yaitu \(x^2-25\) yang mana turunannya sama dengan \(2x\) dan penyebut dari fungsi limitnya yaitu \(x-5\) yang jika diturunkan diperoleh nilai 1.
Dengan demikian, menurut Aturan L'Hospital, kita dapatkan hasil berikut:

Contoh 2:
Hitunglah \( \displaystyle \lim_{x \to \infty} \ \frac{2x}{6x-7} \).
Pembahasan:
Jika kita substitusi nilai \(x = ∞\) ke fungsi limitnya, kita peroleh bentuk tak tentu \(∞/∞\) sehingga kita dapat menerapkan Aturan L'Hospital untuk menyelesaikan limit ini.
Sebenarnya, kita dapat menyelesaikan limit tak hingga ini dengan cara pembagian dengan pangkat tertinggi. Pangkat tertinggi dari fungsi limitnya adalah \(x\), sehingga jika kita bagi pembilang dan penyebut fungsinya dengan \(x\), kita peroleh:

Perlu diingat bahwa kita tidak selalu dapat menggunakan metode pembagian pangkat tertinggi untuk menyelesaikan limit. Jika demikian halnya, kita dapat menggunakan Aturan L'Hospital yakni dengan menurunkan pembilang dan penyebut dari fungsi limitnya dan substitusi nilai \(x\) ke fungsi yang telah diturunkan tersebut, yakni:

Sering kali kita akan perlu menerapkan Aturan L’Hospital lebih dari satu kali hingga diperoleh nilai limit yang diinginkan. Perhatikan dua contoh berikut:
Contoh 3:
Hitunglah \( \displaystyle \lim_{x \to \infty} \ \frac{e^x}{x^2} \).
Pembahasan:
Jika kita substitusi \(x = \infty\) ke fungsi limitnya, kita peroleh hasil tak tentu ∞/∞ sehingga kita dapat menerapkan Aturan L'Hospital untuk menyelesaikan limit ini.
Perhatikan bahwa pembilang dari fungsi limitnya yaitu \(e^x\) di mana kita tahu turunan dari \(e^x\) yaitu \(e^x\) itu sendiri. Untuk penyebut dari fungsi limitnya yaitu \(x^2\), kita dapatkan turunan pertamanya yaitu \(2x\) dan jika diturunkan sekali lagi diperoleh hasil 2.
Dengan demikian, menurut Aturan L'Hospital, kita peroleh:

Contoh 4:
Hitunglah \( \displaystyle \lim_{x \to \infty} \ \frac{x^3 - 4x}{3x^3+x^2} \).
Pembahasan:
Dengan memasukkan \(x = \infty\) ke fungsi limitnya diperoleh bentuk tak tentu ∞/∞ sehingga Aturan L'Hospital dapat dipakai untuk menangani limit ini.
Perhatikan bahwa pembilang dari fungsi limitnya yaitu \(x^3-4x\) di mana turunan pertamanya yaitu \(3x^2 - 4\), turunan keduanya \(6x\), dan turunan ketiganya yaitu 6. Sementara itu, penyebut dari fungsi limitnya yaitu \(3x^3 + x^2\) di mana turunan pertama, kedua, dan ketiganya berturut-turut yaitu \(9x^2+2x, \ 18x+2, \ 18\).
Dengan demikian, menurut Aturan L'Hospital, kita peroleh:
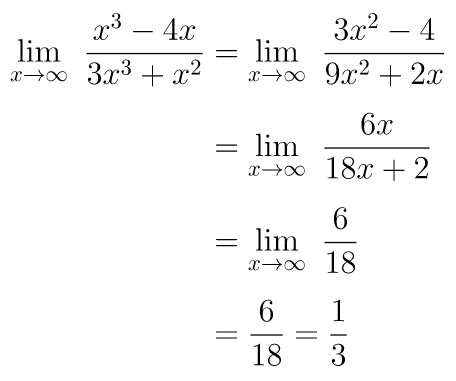
Aturan L’Hospital juga dapat diterapkan untuk limit di mana fungsinya berupa fungsi trigonometri. Perhatikan contoh berikut.
Contoh 5:
Hitunglah \( \displaystyle \lim_{x \to 0} \ \frac{\sin x}{x} \).
Pembahasan:
Dengan substitusi \(x = 0\), kita peroleh bentuk tak tentu 0/0 sehingga kita dapat menerapkan Aturan L'Hospital, yakni:

Contoh 6:
Hitunglah \( \displaystyle \lim_{x \to 0} \ \frac{x \tan x}{\sin 3x} \).
Pembahasan:
Dengan substitusi \(x = 0\), kita peroleh bentuk tak tentu 0/0, yakni

Dengan demikian, Aturan L'Hospital dapat dipakai untuk menyelesaikan limit ini, yakni:

Catatan: Hal yang perlu menjadi perhatian saat menggunakan Aturan L’Hospital yaitu aturan ini tidak dapat dipakai jika limit tersebut hasilnya bukan dalam bentuk tak tentu. Untuk lebih jelasnya, perhatikan contoh berikut:
Contoh 7:
Hitunglah \( \displaystyle \lim_{x \to 3} \ \frac{x^2}{2x-6} \).
Pembahasan:
Jika kita substitusi nilai \(x = 3\) ke fungsi limitnya, kita peroleh hasil:

Hasil dari limit di atas bukan dalam bentuk tak tentu sehingga kita tidak dapat menerapkan Aturan L'Hospital untuk menyelesaikan limit tersebut.
Contoh Soal Aturan L’Hospital Lainnya
Berikut ini diberikan sejumlah contoh soal terkait Aturan L'Hospital.
Contoh 8:
Hitunglah \( \displaystyle \lim_{x \to 0^+} \ x \ \ln x \).
Pembahasan:
Jika kita substitusi \(x = 0\) ke fungsi limitnya, kita peroleh bentuk tak tentu (0) (∞). Aturan L'Hospital tidak dapat diterapkan pada bentuk tak tentu berupa perkalian seperti itu, karena Aturan L'Hospital hanya berlaku pada bentuk tak tentu pembagian, misalnya 0/0 atau ∞/∞.
Akan tetapi, kita dapat memodifikasi fungsi limitnya sehingga diperoleh bentuk tak tentu pembagian. Perhatikan berikut ini:
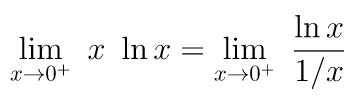
Sekarang, jika kita substitusi \(x = 0\) ke fungsi limit yang telah dimodifikasi ini, kita peroleh bentuk tak tentu ∞/∞ sehingga kita dapat menerapkan Aturan L'Hospital untuk menyelesaikan limit tersebut, yakni:

Jadi, hasil dari \( \displaystyle \lim_{x \to 0^+} \ x \ \ln x = 0 \).
Contoh 9:
Hitunglah \( \displaystyle \lim_{x \to -\infty} \ x \ e^x \).
Pembahasan:
Jika kita substitusi \(x = -∞\) ke fungsi limitnya, kita peroleh bentuk tak tentu (∞)(0). Ini artinya kita perlu memodifikasi fungsi limitnya sehingga diperoleh bentuk tak tentu berupa pembagian 0/0 atau ∞/∞.
Kita bisa tuliskan limit dalam soal ini menjadi:

Sekarang jika kita substitusi \(x = -∞\) ke fungsi limit di atas, kita peroleh bentuk 0/0. Akan tetapi, kita harus hati-hati di sini. Jika kita gunakan Aturan L'Hospital, maka kita dapatkan hasil berikut:

Seperti yang bisa kita lihat dari hasil di atas, penggunaan Aturan L'Hospital tampak tidak berhasil. Kita bisa perbaiki ini dengan memodifikasi fungsi limitnya sehingga menjadi:

Dengan substitusi \(x = -∞\) ke fungsi limit yang baru ini, kita peroleh bentuk ∞/∞ sehingga jika diterapkan Aturan L'Hospital, maka kita peroleh hasil berikut:
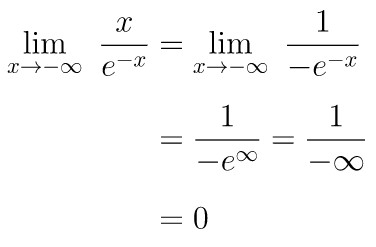
Jadi, hasil dari \( \displaystyle \lim_{x \to -\infty} \ x \ e^x = 0 \).
Contoh 10:
Hitunglah \( \displaystyle \lim_{x \to 0} \ \frac{3^x-2^x}{x^2-x} \).
Pembahasan:
Jika kita substitusi \(x = 0\) ke fungsi limitnya, diperoleh:

Karena ini bentuk tak tentu 0/0, maka kita dapat terapkan Aturan L'Hospital untuk menyelesaikan limit tersebut. Kita peroleh hasil berikut:

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
If you can be anything in this world, be kind.
