www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Rumus Menghitung Luas dan Keliling Beberapa Bangun Ruang Tiga Dimensi dan Contohnya
Rumus Menghitung Luas dan Keliling Beberapa Bangun Ruang Tiga Dimensi dan Contohnya
Ada tujuh bangun ruang yang akan kita pelajari yakni kubus, balok, prisma, limas, tabung, kerucut, dan bola. Tiap-tiap bangun ruang tersebut dapat dihitung luas permukaan dan volumenya.
Pada artikel sebelumnya, kita telah membahas mengenai bangun datar (bangun dua dimensi) yang merupakan salah satu topik bahasan penting dalam goemetri.
Topik penting lainnya terkait geometri yaitu bangun ruang tiga dimensi. Ada tujuh bangun ruang yang akan kita pelajari yakni kubus, balok, prisma, limas, tabung, kerucut, dan bola. Tiap-tiap bangun ruang tersebut dapat dihitung luas permukaan dan volumenya.
Kubus
Kubus merupakan bangun ruang tiga dimensi yang batasi oleh 6 buah persegi atau bujur sangkar yang saling kongruen. Keenam bujur sangkar tersebut disebut sisi kubus dan garis yang menjadi perpotongan dua sisi kubus disebut rusuk kubus. Kubus memiliki 12 rusuk yang sama panjang
Perhatikan gambar kubus berikut ini.
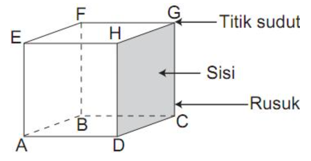
Luas permukaan dan volume dari kubus diberikan oleh
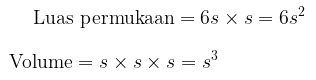
Contoh 1:
Diketahui suatu kubuas ABCD.EFGH mempunyai panjang sisi atau rusuk 6 cm. Tentukan luas permukaan dan volume kubus tersebut.
Pembahasan:
Luas permukaan dan volume dari kubus ABCD.EFGH tersebut adalah

Jadi, luas permukaan dari kubus adalah 216 cm2 dan volumenya 2162
Balok
Balok merupakan bangun ruang tiga dimensi yang memiliki 6 sisi di mana masing-masing sisi yang berhadapan saling kongruen. Balok memiliki 12 rusuk dengan tiga kelompok panjang yang berbeda yang kita sebut panjang (p), lebar (l) dan tinggi (t).
Perhatikan gambar balok berikut ini.

Luas permukaan dan volume dari balok diberikan oleh

Contoh 2:
Sebuah es batu berbentuk balok mempunyai ukuran panjang 80 cm, lebar 15 cm, dan tinggi 20 cm. Hitunglah luas permukaan dan volume dari es batu tersebut.
Pembahasan:

Jadi, luas permukaan es batu adalah 6200 cm2 dan volumenya adalah 24.000 cm3
Prisma
Prisma merupakan bangun ruang tiga dimensi yang mempunyai dua bidang yang sejajar dan kongruen yang disebut penampang. Bidang yang menghubungkan kedua penampang disebut selimut prisma. Terdapat beberapa jenis prisma berdasarkan penampangnya yakni prisma segitiga jika penampangnya berbentuk segitiga, prisma segiempat jika penampangnya segiempat dan seterusnya.
Perhatikan gambar prisma berikut ini.

Luas permukaan dan volume dari prisma diberikan oleh

Contoh 3:
Diketahui prisma segitiga siku-siku seperti tampak pada gambar di bawah.

Tentukan luas permukaan dan volume dari prisma tersebut.
Pembahasan:
Luas permukaan dari prisma di atas merupakan penjumlahan dari luas alas dan luas atas yang berbentuk segitiga siku-siku dan 3 buah luas selimut prisma yang berbentuk persegi panjang.

Limas
Limas merupakan bangun ruang tiga dimensi yang terdiri dari satu bidang alas dan selimut bangun yang berbentuk bidang-bidang segitiga. Pertemuan antara satu titik dari masing-masing segitiga di sebuah titik disebut titik puncak limas.
Perhatikan gambar limas berikut ini.

Luas permukaan dan volume dari limas diberikan oleh

Contoh 4:
Diketahui limas segiempat beraturan seperti tampak pada gambar di bawah.

Tentukan luas permukaan dan volume dari limas tersebut.
Pembahasan:
Luas permukaan dari limas segiempat beraturan tersebut yaitu
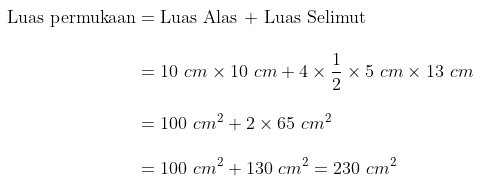
Volume limas tersebut adalah
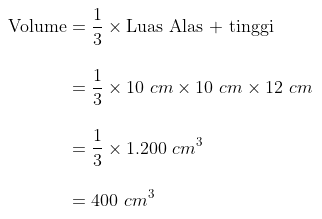
Tabung (Silinder)
Tabung atau silinder merupakan bangun ruang tiga dimensi yang memiliki dua bidang penampang berbentuk lingkaran yang sejajar dan kongruen. Bidang selimut tabung merupakan bidang persegi panjang yang dilengkungkan secara mulus mengikuti keliling penampangnya atau bidang lingkarannya. Tabung dapat disebut juga prisma tegak dengan bidang alas dan atasnya berupa lingkaran.
Perhatikan gambar tabung berikut ini.

Luas permukaan dan volume dari tabung diberikan oleh
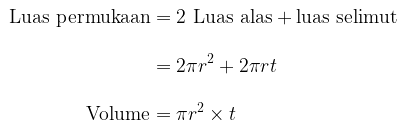
Contoh 5:
Diketahui tabung seperti tampak pada gambar di bawah.
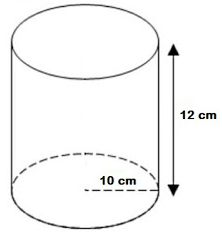
Tentukan luas permukaan dan volume dari tabung tersebut.
Pembahasan:
Dari gambar tabung di atas diperoleh r = 10 cm dan t = 12 cm. Dengan demikian, luas permukaan dan volume tabung tersebut adalah sebagai berikut.

Kerucut
Kerucut merupakan bangun ruang tiga dimensi yang dibatasi oleh bidang alas yang berbentuk lingkaran dan bidang selimut yang berbentuk lengkung mengikuti keliling lingkaran atau bidang alasnya.
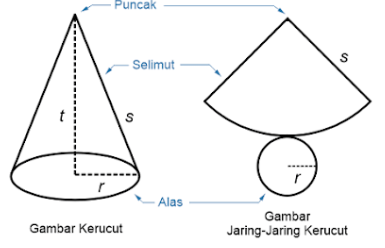
Perhatikan gambar kerucut berikut ini.
Luas permukaan dan volume dari kerucut diberikan oleh
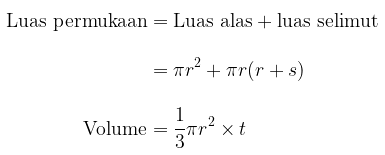
Contoh 6:
Sebuah kerucut, memiliki panjang jari-jari alas sebuah yaitu 5 cm serta tingginya 12 cm. Hitunglah luas permukaan dan volume kerucut tersebut.
Pembahasan:
Perhatikan kembali gambar kerucut pada penjelasan di atas. Hubungan antara r, s, dan t adalah segitiga siku-siku sehingga berlaku teorema pythagoras yakni

Dengan demikian, luas permukaan dan valume dari kerucut tersebut adalah

Bola
Bangun ruang yang satu ini harusnya tidak asing lagi, hampir setiap hari kita melihatnya bahkan mungkin bermain dengannya di lapangan bola. Secara definisi, bola merupakan bangun ruang tiga dimensi yang terbentuk dari himpunan titik dalam dimensi tiga yang memiliki jarak sama terhadap satu titik tertentu yang disebut pusat bola. Jarak pusat bola ke titik-titik permukaan lingkaran disebut jari-jari bola.
Perhatikan gambar bola berikut ini.
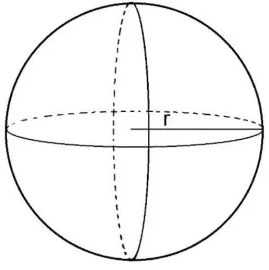
Luas permukaan dan volume dari bola diberikan oleh
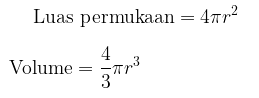
Contoh 7:
Doni di beri sebuah bola oleh ayah nya yang memiliki jari – jari sebesar 30cm, maka carilah volume bola dan luas permukaan bola?
Pembahasan:
Luas permukaan dan volume dari bola tersebut adalah

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Hanya satu cara menghindari kritikan: tidak berbuat apa-apa, tidak berkata apa-apa, dan tidak menjadi apa-apa.
