www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar   »   Turunan Fungsi   ›  Menentukan Interval Fungsi Naik dan Fungsi Turun, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Menentukan Interval Fungsi Naik dan Fungsi Turun, Contoh Soal dan Pembahasan

Salah satu penerapan dari turunan adalah untuk menentukan kapan suatu fungsi naik (increasing), turun (decreasing), atau konstan (constant).

Salah satu penerapan dari turunan adalah untuk menentukan kapan suatu fungsi naik (increasing), turun (decreasing), atau konstan (constant). Istilah naik, turun, dan konstan digunakan untuk menjelaskan perilaku sebuah fungsi ketika bergerak dari kiri ke kanan sepanjang grafiknya.

Sebagai contoh, grafik pada Gambar 1 di bawah dapat dijelaskan sebagai fungsi yang naik pada sebelah kiri \(x = 0\), turun pada \(x = 0\) sampai \(x = 2\) \( (0 < x < 2) \), naik dari \( x = 2\) sampai \(x = 4\) \( (2 < x < 4) \), dan konstan pada sebelah kanan \(x = 4\).

Gambar

Gambar 1. Ilustrasi fungsi naik, turun, dan konstan

Untuk lebih jelasnya, kita nyatakan fungsi naik, fungsi turun, dan fungsi konstan pada definisi berikut.

Definisi: Fungsi Naik, Fungsi Turun, dan Fungsi Konstan

Misalkan fungsi \(f\) terdefinisi pada sebuah interval, dan andaikan \(x_1\) dan \(x_2\) menunjukkan titik pada interval tersebut. Maka

  1. Fungsi \(f\) naik pada interval tersebut jika \(f(x_1) < f(x_2)\) bilamana \(x_1 < x_2\).
  2. Fungsi \(f\) turun pada interval tersebut jika \(f(x_1) > f(x_2)\) bilamana \(x_1 < x_2\).
  3. Fungsi \(f\) konstan pada interval tersebut jika \(f(x_1) = f(x_2)\) utuk semua titi \(x_1\) dan \(x_2\).

Gambar 2 di bawah memberikan ilustrasi mengenai fungsi naik, fungsi turun, dan fungsi konstan sesuai dengan definisi di atas.

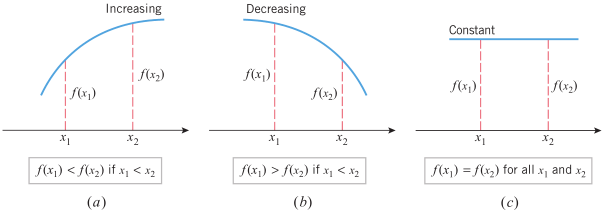
Gambar

Gambar 2. Ilustrasi fungsi naik, turun, dan konstan

Pada artikel sebelumnya kita telah belajar mengenai garis singgung pada kurva. Sekarang perhatikan Gambar 3 di bawah yang menunjukkan kaitan antara fungsi naik, fungsi turun, dan konstan dengan garis singgung (tangent line) suatu kurva.

Gambar

Gambar 3. Kaitan fungsi naik, turun, dan konstan dengan garis singgung

Gambar 3 di atas menunjukkan bahwa sebuah fungsi \(f\) yang terdiferensialkan akan naik pada interval di mana tiap-tiap garis singgung pada grafiknya mempunyai kemiringan positif (has positive slope), akan turun pada interval di mana garis singgung pada grafiknya mempunyai kemiringan negatif (has negative slope), dan konstan pada interval di mana garis singgung pada grafiknya mempunyai kemiringan nol (has zero slope).

Observasi intuitif ini dapat dinyatakan dalam teorema penting berikut ini.

Teorema:

Andaikan fungsi \(f\) adalah fungsi yang kontinu pada interval tertutup \( [a,b] \) dan terdiferensialkan pada interval terbuka (a,b). Maka

  1. Jika \(f'(x) > 0\) untuk setiap nilai \(x\) pada \((a,b)\), maka fungsi \(f\) naik pada \([a,b]\).
  2. Jika \(f'(x) < 0\) untuk setiap nilai \(x\) pada \((a,b)\), maka fungsi \(f\) turun pada \([a,b]\).
  3. Jika \(f'(x) = 0\) untuk setiap nilai \(x\) pada \((a,b)\), maka fungsi \(f\) konstan pada \([a,b]\).

Meskipun dinyatakan untuk interval tertutup, teorema di atas juga berlaku untuk setiap interval di mana fungsi \(f\) kontinu. Misalnya, jika fungsi \(f\) kontinu pada \([a, +∞)\) dan \(f'(x) > 0 \) pada \((a, +∞)\), maka fungsi \(f\) turun pada \([a, +∞)\); dan jika fungsi \(f\) kontinu pada \( (-∞, +∞) \) dan \(f'(x) < 0 \) pada \( (-∞, +∞) \), maka fungsi \(f\) turun pada \( (-∞, +∞) \).

Contoh 1:

Carilah interval di mana fungsi \( f(x) = x^2 - 4x + 3 \) naik dan interval di mana fungsinya turun.

Pembahasan »

Perhatikan grafik untuk fungsi \( f(x) = x^2 - 4x + 3 \) di bawah yang menunjukkan bahwa fungsi \(f\) turun untuk semua \(x \leq 2\) dan menaik pada \( x \geq 2 \).

Gambar

Untuk mengonfirmasi ini, kita akan analisis turunan fungsi tersebut. Turunan dari \(f\) yaitu

Gambar

Dengan demikian,

Gambar

Karena \(f\) adalah kontinu di mana-mana, maka \(f\) akan turun pada interval \( (-\infty, 2] \) dan naik pada interval \( [2, +\infty] \).

Kesimpulan ini konsisten dengan grafik \(f\) pada Gambar di atas.

Contoh 2:

Carilah interval di mana fungsi \( f(x) = x^3 \) naik dan interval di mana fungsinya turun.

Pembahasan »

Perhatikan grafik untuk fungsi \( f(x) = x^3 \) di bawah yang menunjukkan bahwa fungsi \(f\) naik sepanjang sumbu-x.

Gambar

Untuk mengonfirmasi ini, kita akan mencari turunan fungsi tersebut. Dari hasil perhitungan diperoleh \( f'(x) = 3x^2 \). Dengan demikian,

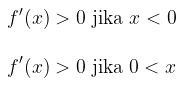
Gambar

Karena \(f\) adalah kontinu di mana-mana, dan f naik pada interval \( (-\infty, 0] \) dan naik pada interval \( [0, +\infty] \), maka \(f\) naik pada interval \( (-\infty, +\infty) \).

Kesimpulan ini konsisten dengan grafik \(f\) pada Gambar di atas.

Contoh 3: UM UGM 2005

Jika diberikan fungsi \(f\) dengan rumus \( f(x) = x \sqrt{x+1} \) maka daerah dengan fungsi \(f\) naik adalah…

  1. \( \displaystyle -1 \leq x \leq -\frac{2}{3} \)
  2. \( \displaystyle x \leq -1 \)
  3. \( \displaystyle -1 \leq x < -\frac{2}{3} \)
  4. \( \displaystyle x > -\frac{2}{3} \)
  5. \( \displaystyle x > \frac{2}{3} \)
Pembahasan »

Ingat bahwa syarat suatu fungsi \(f(x)\) akan naik adalah ketika \( f’(x) > 0 \) sehingga langkah pertama yang akan kita lakukan adalah mencari turunan pertama dari fungsi \(f(x)\). Kita bisa bisa mencari turunan \( f(x) \) menggunakan rumus aturan perkalian. Berikut hasil yang kita peroleh:

\begin{aligned} f(x) &= x \sqrt{x+1} = x (x+1)^{\frac{1}{2}} \\[8pt] u &= x \Leftrightarrow u' = 1 \\[8pt] v &= (x+1)^{\frac{1}{2}} \Leftrightarrow v' = \frac{1}{2}(x+1)^{-\frac{1}{2}} \\[8pt] f'(x) &= u' \cdot v + u \cdot v' \\[8pt] &= 1 \cdot (x+1)^{\frac{1}{2}} + x \cdot \frac{1}{2}(x+1)^{-\frac{1}{2}} \\[8pt] &= (x+1)^{\frac{1}{2}} + \frac{x}{2(x+1)^{\frac{1}{2}}} \\[8pt] &= \frac{2(x+1)+x}{2(x+1)^{\frac{1}{2}}} = \frac{3x+2}{2(x+1)^{\frac{1}{2}}} \end{aligned}

Selanjutnya, untuk \( f’(x) > 0 \), kita peroleh:

\begin{aligned} f'(x) > 0 \Leftrightarrow \frac{3x+2}{2(x+1)^{\frac{1}{2}}} > 0 \\[8pt] \frac{3x+2}{2\sqrt{x+1}} > 0 \end{aligned}

Untuk setiap \(x\) bilangan real, hasil dari \( 2\sqrt{x+1} \) adalah bilangan real positif, sehingga agar \( \displaystyle \frac{3x+2}{2\sqrt{x+1}} > 0 \) atau \( \frac{3x+2}{(+)} > 0 \) maka pembilang \((3x+2)\) harus bilangan real positif. Dapat kita tuliskan \( 3x + 2 > 0 \) atau \( \displaystyle x > -\frac{2}{3}\).

Jawaban D.

Contoh 4: SIMAK UI 2009

Jika kurva \( y = (x^2-a)(2x+b)^3 \) turun pada interval \( -1 < x < \frac{2}{5} \), maka nilai \(ab = \cdots \)

  1. \( -3 \)
  2. \( -2 \)
  3. \( 1 \)
  4. \( 2 \)
  5. \( 3 \)
Pembahasan »

Untuk menentukan turunan pertama kita pakai aturan perkalian turunan, yakni untuk \( y = u \cdot v \) maka \( y’ = u’ \cdot v + u \cdot v’ \). Kita peroleh hasil berikut:

\begin{aligned} y &= (x^2-a)(2x+b)^3 \\[8pt] u &= (x^2-a) \Leftrightarrow u'=2x \\[8pt] v &= (2x+b)^3 \Leftrightarrow v' = 6(2x+b)^2 \\[8pt] y &= u \cdot v \Leftrightarrow y' = u' \cdot v + u \cdot v' \\[8pt] y' &= 2x \cdot (2x+b)^3 + (x^2-a) \cdot 6(2x+b)^2 \\[8pt] &= (2x+b)^2 \ [2x \cdot (2x+b) + 6(x^2-a)] \\[8pt] &= (2x+b)^2 [4x^2+2bx+6x^2-6a] \\[8pt] &= (2x+b)^2 (10x^2+2bx-6a) \end{aligned}

Ingat bahwa syarat kurva suatu fungsi akan turun adalah ketika \( y’ < 0 \) sehingga kita peroleh:

\begin{aligned} y' < 0 \Leftrightarrow (2x+b)^2 \ (10x^2+2bx-6a) &< 0 \\[8pt] 2 (2x+b)^2 \ (5x^2+bx-3a) &< 0 \end{aligned}

Dari pertidaksamaan di atas kita ketahui bahwa \( 2(2x+b)^2 \geq 0 \) untuk setiap bilangan real sehingga berlaku \( (5x^2+bx-3a) < 0 \).

Himpunan penyelesaian dari \( (5x^2+bx-3a) < 0 \) adalah \( -1 < x < \frac{2}{5} \) sehingga berlaku:

\begin{aligned} x < \frac{2}{5} &\Leftrightarrow (5x-2) < 0 \\[8pt] x > -1 &\Leftrightarrow (x+1) > 0 \end{aligned}

Untuk \( (5x-2) < 0 \) dan \( (x+1) > 0 \), kita peroleh:

\begin{aligned} (5x-2)(x+1) < 0 \\[8pt] 5x^2+5x-2x-2 < 0 \\[8pt] 5x^2+3x-2 < 0 \\[8pt] 5x^2+bx-3a < 0 \\[8pt] b = 3 \quad \text{dan} \quad a = \frac{2}{3} \\[8pt] ab = \frac{2}{3} \cdot 3 = 2 \end{aligned}

Jawaban D.

Contoh 5: SPMB 2004 Regional III

Fungsi \( f(x) = 4x^3-9x^2-12x+1 \) turun untuk nilai \(x\) yang memenuhi…

  1. \( x < -2 \)
  2. \( -2 < x < \frac{1}{2} \)
  3. \( -2 < x < 2 \)
  4. \(x > 2\)
  5. \( -\frac{1}{2} < x < 2 \)
Pembahasan »

Syarat suatu fungsi \(f(x)\) akan turun adalah ketika \( f’(x) < 0 \) sehingga kita peroleh hasil berikut:

\begin{aligned} f(x) &= 4x^3-9x^2-12x+1 \\[8pt] f'(x) &= 12x^2-18x-12 \\[8pt] f'(x) < 0 &\Leftrightarrow 12x^2-18x-12 < 0 \\[8pt] &\Leftrightarrow 2x^2-3x-2 < 0 \\[8pt] &\Leftrightarrow (2x+1)(x-2) < 0 \\[8pt] &\Leftrightarrow x = -\frac{1}{2} \quad \text{atau} \quad x = 2 \end{aligned}

Jadi, fungsi \( f(x) = 4x^3-9x^2-12x+1 \) turun pada interval \( \displaystyle -\frac{1}{2} < x < 2 \).

Jawaban E.

Contoh 6: SPMB 2006

Grafik \( y = 2x^3-\frac{5}{2}x^2-6x+5 \) naik untuk \(x\) yang memenuhi…

  1. \( \frac{3}{2} < x < \frac{5}{2} \)
  2. \( -\frac{3}{2} < x < \frac{3}{2} \)
  3. \( -\frac{3}{2} < x < \frac{5}{2} \)
  4. \(x < -\frac{2}{3}\) atau \( x > \frac{3}{2} \)
  5. \(x < -\frac{2}{3}\) atau \( x > \frac{5}{2} \)
Pembahasan »

Syarat suatu grafik fungsi \(f(x)\) akan naik adalah saat \( f’(x) > 0 \) sehingga kita peroleh hasil berikut:

\begin{aligned} f(x) &= 2x^3-\frac{5}{2}x^2-6x+5 \\[8pt] f'(x) &= 6x^2-5x-6 \\[8pt] f'(x) < 0 &\Leftrightarrow 6x^2-5x-6 < 0 \\[8pt] &\Leftrightarrow (2x-3)(3x+2) < 0 \\[8pt] &\Leftrightarrow \text{pembuat nolnya, yaitu:} \\[8pt] &\Leftrightarrow x = \frac{3}{2} \quad \text{atau} \quad x = -\frac{2}{3} \end{aligned}

Jadi, grafik \( y = 2x^3-\frac{5}{2}x^2-6x+5 \) naik pada interval \( x < - \frac{2}{3} \) atau \( x > \frac{3}{2} \).

Jawaban D.

Contoh 7: UNBK Matematika SMA IPS 2019

Grafik fungsi \( f(x) = x^3+\frac{3}{2}x^2-18x+5 \) naik pada interval…

  1. \( -2 < x < 3 \)
  2. \( -3 < x < 2 \)
  3. \( x < 2 \) atau \( x > 3 \)
  4. \( x < -3 \) atau \( x > 2 \)
  5. \( x < -2 \) atau \( x > 3 \)
Pembahasan »

Untuk menentukan interval nilai \(x\) agar fungsi \( f(x) = x^3+\frac{3}{2}x^2-18x+5 \) naik, kita cukup menentukan interval nilai \(x\) yang memenuhi \(f’(x) > 0\).

\begin{aligned} f(x) &= x^3+\frac{3}{2}x^2-18x+5 \\[8pt] f'(x) &= 3x^2-3x-18 \\[8pt] f'(x) < 0 &\Leftrightarrow 3x^2-3x-18 < 0 \\[8pt] &\Leftrightarrow x^2-x-6 < 0 \\[8pt] &\Leftrightarrow (x-3)(x+2) < 0 \\[8pt] &\Leftrightarrow \text{pembuat nolnya, yaitu:} \\[8pt] &\Leftrightarrow x = 3 \quad \text{atau} \quad x = -2 \end{aligned}

Nilai \(x\) yang memenuhi pertidaksamaan di atas adalah \( x < -2\) atau \( x > 3\). Dengan demikian, grafik fungsi \( f(x) = x^3+\frac{3}{2}x^2-18x+5 \) akan naik ketika \( x < -2\) atau \( x > 3\).

Jawaban E.

Contoh 8: SPMB 2004 Regional I

Fungsi \( f(x) = \frac{x^2+3}{x-1} \) turun untuk nilai \(x\) yang memenuhi…

  1. \( -3 < x < 1 \)
  2. \( -3 < x < 1 \) atau \( x > 1 \)
  3. \( -1 < x < 1 \) atau \( 1 < x < 3 \)
  4. \( x < -3 \) atau \(x > 1\)
  5. \( x < -1 \) atau \( x > 4 \)
Pembahasan »

Ingat bahwa syarat suatu fungsi turun adalah ketika \( f’(x) < 0 \) sehingga kita cari turunan pertama dari fungsi \(f(x)\) terlebih dahulu. Untuk mencari turunan dari \( f(x) = \frac{x^2+3}{x-1} \) kita bisa gunakan rumus aturan pembagian turunan. Berikut hasil yang kita peroleh:

\begin{aligned} f(x) &= \frac{x^2+3}{x-1} \\[8pt] u &= x^2 + 3 \Leftrightarrow u' = 2x \\[8pt] v &= x-1 \Leftrightarrow v' = 1 \\[8pt] f'(x) &= \frac{u' \cdot v - u \cdot v'}{v^2} \\[8pt] &= \frac{2x \cdot (x-1) -(x^2+3) \cdot 1 }{(x-1)^2} \\[8pt] &= \frac{2x^2-2x-x^2-3}{(x-1)^2} = \frac{x^2-2x-3}{(x-1)^2} \\[8pt] &= \frac{(x-3)(x+1)}{(x-1)^2} \end{aligned}

Selanjutnya, kita akan mencari interval \(x\) yang memenuhi \( f’(x) < 0 \) atau \( \frac{(x-3)(x+1)}{(x-1)^2} < 0 \). Untuk mendapatkan nilai \(x\) yang memenuhi pada pertidaksamaan kita lakukan uji titik dengan batasan nilai \(x\), pembuat nol pada pembilang dan penyebut yaitu \( x = -1, x = 1 \) dan \(x=3\). Berikut hasil yang kita peroleh:

Dari hasil di atas kita peroleh nilai \(x\) yang memenuhi pertidaksamaan \( \frac{(x-3)(x+1)}{(x-1)^2} < 0 \) yaitu \( -1 < x < 1 \) atau \(1 < x < 3\).

Jawaban C.

Contoh 9:

Fungsi \( f(x) = \sin x-\cos x \) untuk \( 0 < x < 2\pi \) naik pada interval….

  1. \( 0 < x < \frac{\pi}{4} \)
  2. \( \frac{\pi}{4} < x < 2\pi \)
  3. \( \frac{3\pi}{4} < x < \frac{7\pi}{4} \)
  4. \( 0 < x < \frac{3\pi}{4} \) atau \( \frac{7\pi}{4} < x < 2\pi \)
  5. \( 0 < x < \frac{\pi}{4} \) atau \( \frac{3\pi}{4} < x < 2\pi \)
Pembahasan »

Syarat suatu grafik fungsi akan naik yaitu turunan pertama lebih dari nol atau \( f’(x) > 0 \). Turunan pertama dari \(f(x) = \sin x-\cos x \) yaitu \( f’(x) = \cos x + \sin x \) sehingga:

\begin{aligned} f'(x) &> 0 \\[8pt] \cos x + \sin x &> 0 \\[8pt] \end{aligned}

Untuk menyelesaikan pertidaksamaan trigonometri di atas, kita tentukan pembuat nolnya terlebih dahulu pada interval \( 0 < x < 2\pi \) yakni:

\begin{aligned} \cos x + \sin x &= 0 \\[8pt] x = \{ 135^\circ, 315^\circ \} \ &\text{atau} \ x = \left\{ \frac{3\pi}{4}, \frac{7\pi}{4} \right\} \end{aligned}

Dari hasil di atas, kita bisa buat suatu garis bilangan. Setelah itu, tentukan tanda +/- pada interval-interval tersebut dengan uji titik yakni dengan mengambil sembarang nilai \(x\) yang terletak di dalam interval tersebut dan substitusikan pada \( f’(x) = \cos x + \sin x \).

Karena syarat fungsi naik adalah \( f’(x) > 0 \), maka interval yang memenuhi adalah yang bertanda positif atau fungsi \(f(x) = \sin x-\cos x\) naik pada interval \( 0 < x < \frac{3\pi}{4} \) atau \( \frac{7\pi}{4} < x < 2\pi \).

Jawaban D.

Contoh 10:

Diketahui fungsi \( f(x)=\sin \left( x-\frac{\pi}{3} \right) \) dengan \( 0 < x < 2\pi \). Kurva fungsi \( f(x) \) akan cekung ke bawah pada interval…

  1. \( 0 < x < \frac{\pi}{3} \)
  2. \( 0 < x < \frac{\pi}{3} \) atau \( \frac{4\pi}{3} < x < \frac{7\pi}{3} \)
  3. \( 0 < x < \pi \)
  4. \( \frac{\pi}{3} < x < \frac{4\pi}{3} \)
  5. \( \frac{\pi}{3} < x < \frac{4\pi}{3} \) atau \( \frac{5\pi}{3} < x < 2\pi \)
Pembahasan »

Syarat fungsi cekung ke bawah yaitu \( f’’(x) < 0 \) yakni turunan kedua dari fungsi \(f(x)\) kurang dari nol. Turunan kedua dari \(f(x)\), yaitu:

\begin{aligned} f(x) &=\sin \left( x-\frac{\pi}{3} \right) \\[8pt] f'(x) &= \cos \left( x-\frac{\pi}{3} \right) \\[8pt] f''(x) &= -\sin \left( x-\frac{\pi}{3} \right) \end{aligned}

Dengan demikian, untuk \( f’’(x) > 0 \), maka:

\begin{aligned} f''(x) &< 0 \\[8pt] -\sin \left( x-\frac{\pi}{3} \right) &< 0 \\[8pt] \sin \left( x-\frac{\pi}{3} \right) &> 0 \end{aligned}

Nilai \(x\) pada interval \( 0 < x < 2\pi \) yang memenuhi pertidaksamaan di atas berada pada interval \( \frac{\pi}{3} < x < \frac{4\pi}{3} \). Dengan demikian, fungsi \( f(x) \) cekung ke bawah pada interval tersebut.

Jawaban D.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel Terkait
img

Nilai maksimum dan nilai minimum suatu fungsi


Somewhere in the world someone is training when you are not. When you race him, he will win.

Tom Fleming