www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar   »   Pertidaksamaan   ›  Pertidaksamaan Hasil Bagi: Rumus, contoh soal dan pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Pertidaksamaan Hasil Bagi: Rumus, contoh soal dan pembahasan

Pertidaksamaan hasil bagi dua polinom adalah pertidaksamaan yang berbentuk pecahan di mana penyebutnya memuat suatu variabel.

Pada artikel ini kita akan membahas cara menyelesaikan atau mencari himpunan penyelesaian dari suatu pertidaksamaan yang berupa hasil bagi dua polinom (suku banyak) atau pertidaksamaan rasional.

Sekarang perhatikan dua pertidaksamaan dalam bentuk pecahan berikut ini:

Gambar

Apakah dua pertidaksamaan di atas termasuk pertidaksamaan hasil bagi atau pertidaksamaan rasional? Tentu saja tidak. Pertidaksamaan pertama bukan pertidaksamaan hasil bagi atau rasional karena penyebut pada pertidaksamaan berupa konstanta atau bukan suatu variabel.

Sedangkan, pertidaksamaan kedua termasuk pertidaksamaan hasil bagi atau rasional karena penyebut pada pertidaksamaan tersebut memuat suatu variabel. Jadi, dapat kita simpulkan bahwa pertidaksamaan hasil bagi atau rasional adalah pertidaksamaan yang berbentuk pecahan di mana penyebutnya memuat suatu variabel.

Jenis-jenis Pertidaksamaan Hasil Bagi

Pada umumnya, pertidaksamaan hasil bagi atau pertidaksamaan pecahan dapat dibagi menjadi dua, yakni:

  1. Pertidaksamaan hasil bagi linear. Bentuk umum pertidaksamaan linear ini berupa
    2. Gambar

    Perhatikan bahwa tanda "<" dapat diganti dengan tanda pertidaksamaan yang lain (>, ≥, atau ≤)

  2. Pertidaksamaan hasil bagi kuadrat, yakni pertidaksamaan hasil bagi yang memuat bentuk kuadrat baik pada pembilang atau penyebut pertidaksamaan atau pada pembilang dan penyebutnya sekaligus. Perhatikan pertidaksamaan hasil bagi kuadrat berikut:
    3. Gambar

    Sekali lagi bahwa kita dapat mengganti tanda "<" dengan tanda pertidaksamaan yang lain (>, ≥, atau ≤)

Sifat-sifat Pertidaksamaan Hasil Bagi

Untuk menyelesaikan pertidaksamaan hasil bagi, penting untuk Anda mengingat kembali sifat-sifat dalam pembagian. Kita nyatakan sebagai berikut:

Gambar

Dari sifat-sifat pembagian yang diberikan di atas, maka kita peroleh sifat-sifat pertidaksamaan hasil bagi sebagai berikut:

  1. Untuk \( \frac{f(x)}{g(x)} > 0 \) dan \( \frac{f(x)}{g(x)} ≥ 0 \) akan berkaitan dengan sifat pembagian \( \frac{(+)}{(+)} = (+) \) dan \( \frac{(-)}{(-)} = (+) \). Artinya, agar \( \frac{f(x)}{g(x)} \) bernilai positif (> 0), maka \(f(x)\) dan \(g(x)\) harus sama-sama bernilai positif atau sama-sama bernilai negatif. Selain itu, karena \( \frac{f(x)}{0} \) adalah tidak terdefinisi, maka syarat untuk \( \frac{f(x)}{g(x)} \) adalah \( g(x) \neq 0 \). Dengan demikian, kita peroleh definisi sebagai berikut:

    2. Definisi 1:

    Jika \( \frac{f(x)}{g(x)} > 0 \), maka \( f(x) > 0 \) dan \( g(x) > 0 \) atau \( f(x) < 0 \) dan \( g(x) < 0 \)

    Jika \( \frac{f(x)}{g(x)} ≥ 0 \), maka \( f(x) ≥ 0 \) dan \( g(x) > 0 \) atau \( f(x) ≤ 0 \) dan \( g(x) < 0 \)

  2. Untuk \( \frac{f(x)}{g(x)} < 0 \) dan \( \frac{f(x)}{g(x)} ≤ 0 \) akan berkaitan dengan sifat pembagian \( \frac{(+)}{(-)} = (-) \) dan \( \frac{(-)}{(+)} = (-) \). Artinya, agar \( \frac{f(x)}{g(x)} \) bernilai negatif (< 0), maka \(f(x)\) dan \(g(x)\) harus memiliki tanda yang berbeda yakni salah satu harus positif dan yang lainnya harus negatif. Selain itu, karena \( \frac{f(x)}{0} \) adalah tidak terdefinisi, maka syarat untuk \( \frac{f(x)}{g(x)} \) adalah \( g(x) \neq 0 \). Dengan demikian, kita peroleh definisi sebagai berikut:

    3. Definisi 2:

    Jika \( \frac{f(x)}{g(x)} < 0 \), maka \( f(x) > 0 \) dan \( g(x) < 0 \) atau \( f(x) < 0 \) dan \( g(x) > 0 \)

    Jika \( \frac{f(x)}{g(x)} ≤ 0 \), maka \( f(x) ≥ 0 \) dan \( g(x) > 0 \) atau \( f(x) ≤ 0 \) dan \( g(x) < 0 \)

Langkah-langkah Menyelesaikan Pertidaksamaan Hasil Bagi

Untuk menyelesaikan pertidaksamaan hasil bagi, ikuti beberapa langkah berikut:

Langkah 1: Pindahkan seluruh suku ke dalam satu ruas atau buatlah ruas kanan pertidaksamaan menjadi nol. Dalam beberapa kasus, langkah pertama ini tidak perlu dilakukan karena ruas kanan pertidaksamaan telah bernilai nol.

Langkah 2: Lakukan operasi aljabar atau lakukan pemfaktoran dengan tujuan untuk menyederhanakan bentuk pertidaksamaan. Dalam beberapa kasus, tidak dapat atau tidak perlu dilakukan operasi aljabar sehingga anda dapat melewati langkah kedua ini.

Langkah 3: Cari nilai \(x\) yang memenuhi berdasarkan sifat-sifat pembagian atau yang telah dinyatakan pada Definisi 1 dan Definisi 2 di atas. Lalu, tuliskan semua nilai \(x\) yang diperoleh tersebut pada garis bilangan.

Langkah 4: Ambil sembarang titik-titik uji pada garis bilangan yang diperoleh dari Langkah 3 dan substitusikan nilai titik-titik uji tersebut pada pertidaksamaan hasil bagi untuk memperoleh tanda yang sesuai (+ atau -).

Langkah 5: Tentukan himpunan penyelesaian dengan mengambil irisan dari nilai \(x\) yang diperoleh pada Langkah 3 atau dengan melihat tanda sesuai titik-titik uji pada Langkah 4.

Contoh 1:

Selesaikan pertidaksamaan \( \frac{(x-1)}{(x+2)} ≥ 0 \).

Pembahasan:

Langkah 1: Kita tidak perlu melakukan langkah 1, karena ruas kanan pertidaksamaan telah bernilai nol.

Langkah 2: Kita dapat melewati langkah dua, karena pertidaksamaan sudah dalam bentuk paling sederhana atau tidak dapat/tidak perlu dilakukan operasi aljabar (pemfaktoran) lagi.

Langkah 3: Berdasarkan Definisi 1 yang telah dijelaskan sebelumnya, maka diperoleh nilai \(x\) sebagai berikut:

\begin{aligned} f(x) = x - 1 &\geq 0 \ \quad \text{atau} \ \quad g(x)=x+2 > 0 \\[8pt] x &\geq 1 \ \quad \text{atau} \ \quad x > -2 \\[8pt] \text{dan} f(x) = x - 1 &\leq 0 \ \quad \text{atau} \ \quad g(x)=x+2 < 0 \\[8pt] x &\leq 1 \ \quad \text{atau} \ \quad x < -2 \end{aligned}

Garis bilangan dari nilai \(x\) yang diperoleh di atas dapat dilihat pada Gambar 1.

Langkah 4: Daerah penyelesaian dapat dilihat pada Gambar 1 berikut. Perhatikan bahwa kita ambil sembarang titik uji -3, 0 dan 2, sehingga diperoleh tanda pertidaksamaan seperti terlihat pada Gambar 1.

Gambar

Gambar 1. Titik uji pada garis bilangan beserta nilainya

Lambang \(u\) (unidentified) menunjukkan bahwa hasil bagi tak terdefinisi di -2.

Langkah 5: Berdasarkan beberapa langkah di atas, maka himpunan penyelesaian untuk pertidaksamaan hasil bagi \( \frac{(x-1)}{(x+2)} ≥ 0 \) adalah \( (-∞,-2)∪[1,∞) \). Perhatikan Gambar 2 berikut:

Gambar

Gambar 2. Daerah untuk himpunan penyelesaian pertidaksamaan

Contoh 2: SBMPTN 2019

Himpunan penyelesaian pertidaksamaan \( \frac{3x}{2-x} < 3 \) adalah…

  1. \( x < 1 \) atau \(x > 2\)
  2. \( x < 2 \) atau \(x > 6\)
  3. \( 1 < x < 2 \)
  4. \( 1 < x < 6 \)
  5. \( x > 2 \)
Pembahasan »

Lakukan operasi aljabar untuk membuat ruas kanan pertidaksamaan menjadi nol.

\begin{aligned} \frac{3x}{2-x} &< 3 \\[8pt] \frac{3x}{2-x}-3 &< 0 \\[8pt] \frac{3x}{x-2}+3 &> 0 \\[8pt] \frac{3x}{x-2}+\frac{3(x-2)}{x-2} &> 0 \\[8pt] \frac{6x-6}{x-2} &> 0 \end{aligned}

Syarat pertama dari pertidaksamaan pecahaan adalah \( x-2 \neq 0 \) sehingga \( x \neq 2 \). Selanjutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:

  • Pembuat nol pembilang: \( 6x-6 = 0 \) maka \(x = 1\)
  • Pembuat nol penyebut: \(x-2 = 0\) maka \(x = 2\).

Tuliskan nilai-nilai \(x\) pembuat nol pada garis bilangan dan lakukan titik uji pada tiap-tiap interval bilangan sehingga kita peroleh berikut:

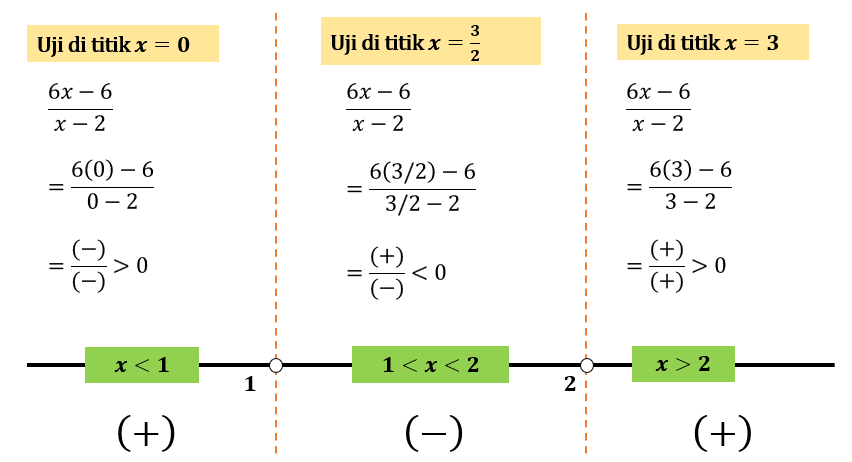
pertidaksamaan pecahan

Dari gambar dapat kita ambil kesimpulan bahwa daerah \(x < 1\) atau \(x > 2\) merupakan himpunan penyelesaian soal karena pada daerah ini \( \frac{6x-6}{x-2} > 0 \).

Jawaban A.

Contoh 3: SBMPTN 2019

Jika \(a < x < b\) adalah solusi dari \( \frac{x^2+x+3}{x^2-x-2} < 0 \), maka nilai \(b-2a\) adalah…

  1. \( 1 \)
  2. \( 2 \)
  3. \( 3 \)
  4. \( 4 \)
  5. \( 5 \)
Pembahasan »

Agar pertidaksamaan pecahan \( \frac{x^2+x+3}{x^2-x-2} < 0 \) mempunyai solusi maka syarat pertama adalah:

\begin{aligned} x^2-x-2 &\neq 0 \\[8pt] (x-2)(x+1) &\neq 0 \\[8pt] x \neq 2 \ \text{atau} \ x &\neq -1 \end{aligned}

Perhatikan bahwa \( x^2+x+3 \) adalah definit positif artinya selalu bernilai positif untuk setiap \(x\) bilangan real.

Selanjutnya, lakukan uji titik \(x\) pada tiap-tiap interval bilangan terhadap ruas kiri pertidaksamaan sehingga diperoleh berikut:

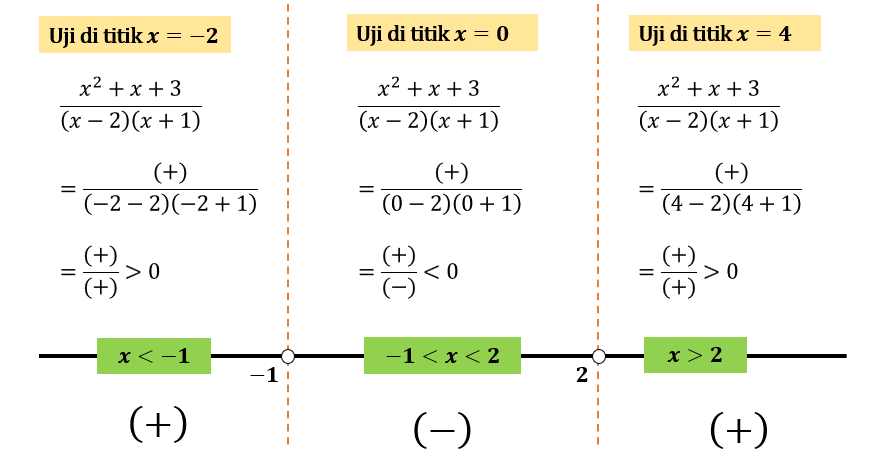
pertidaksamaan pecahan

Himpunan penyelesaian dari pertidaksamaan adalah hasil dari uji titik \(x\) yang memberikan nilai negatif atau kurang dari nol yaitu pada interval \(-1 < x < 2\).

Karena \( -1 < x < 2 \) ekuivalen dengan \( a < x < b\) untuk \(a = -1\) dan \(b = 2\) sehingga diperoleh \(b-2a = 2-2(-1)= 4\).

Jawaban D.

Contoh 4: SBMPTN 2019

Jika \( a < x < b \) adalah solusi dari \( \frac{x^2+2x+2}{x^2+x} < 0 \) maka nilai \(a+b\) adalah…

  1. \( 2 \)
  2. \( 1 \)
  3. \( 0 \)
  4. \( -1 \)
  5. \( -2 \)
Pembahasan »

Agar pertidaksamaan pecahan \( \frac{x^2+2x+2}{x^2+x} < 0 \) mempunyai solusi maka syarat pertama adalah:

\begin{aligned} x^2+x &\neq 0 \\[8pt] x(x+1) &\neq 0 \\[8pt] x \neq 0 \ \text{atau} \ x &\neq -1 \end{aligned}

Perhatikan bahwa \( x^2+2x+2 \) adalah definit positif artinya selalu bernilai positif untuk setiap \(x\) bilangan real.

Selanjutnya, lakukan uji titik \(x\) pada tiap-tiap interval bilangan terhadap ruas kiri pertidaksamaan sehingga diperoleh berikut:

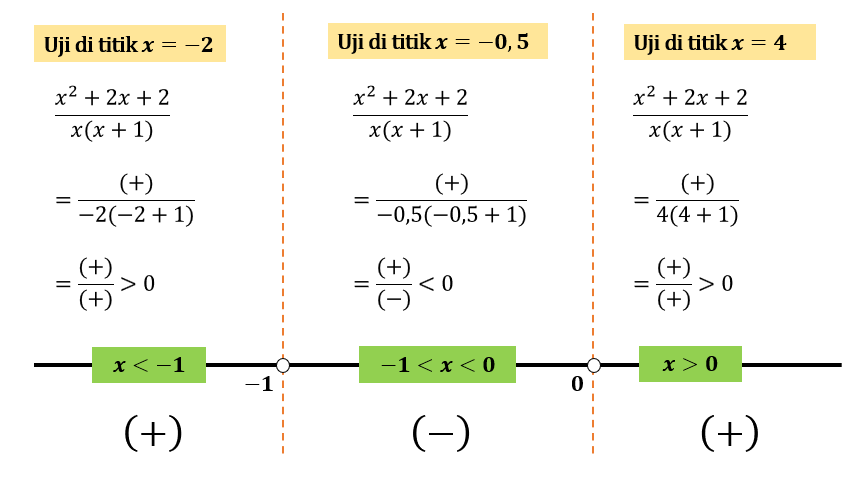
pertidaksamaan pecahan

Himpunan penyelesaian dari pertidaksamaan adalah hasil dari uji titik \(x\) yang memberikan nilai negatif atau kurang dari nol yaitu pada interval \(-1 < x < 0\).

Karena \( -1 < x < 0 \) ekuivalen dengan \( a < x < b\) untuk \(a = -1\) dan \(b = 0\) sehingga diperoleh \(a+b = -1 + 0= -1\).

Jawaban D.

Contoh 5: SBMPTN 2014

Semua nilai \(p\) yang memenuhi pertidaksamaan \( \frac{p}{p-2} \leq \frac{p-1}{p+2} \) adalah…

  1. \( p>2 \) atau \( p<-2 \)
  2. \( -2 < p \leq \frac{2}{5} \) dan \( p \neq 0 \)
  3. \( p < -2 \) atau \( \frac{2}{5} \leq p < 2 \)
  4. \( \frac{2}{5} \leq p < 2 \) dengan \( p \neq 0 \)
  5. \( -2 < p \leq \frac{2}{5} \) atau \( p > 2 \)
Pembahasan »

Lakukan operasi aljabar untuk membuat ruas kanan pertidaksamaan menjadi nol.

\begin{aligned} \frac{p}{p-2} &\leq \frac{p-1}{p+2} \\[8pt] \frac{p}{p-2}-\frac{p-1}{p+2} &\leq 0 \\[8pt] \frac{p(p+2)}{(p-2)(p+2)}-\frac{(p-1)(p-2)}{(p-2)(p+2)} &\leq 0 \\[8pt] \frac{p^2+2p-p^2+3p-2}{(p-2)(p+2)} &\leq 0 \\[8pt] \frac{5p-2}{(p-2)(p+2)} &\leq 0 \end{aligned}

Syarat pertama dari pertidaksamaan di atas adalah \( (p-2)(p+2) \neq 0 \) sehingga diperoleh \( p \neq 2 \) dan \( p \neq -2 \).

Berikutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:

  • Pembuat nol pembilang: \( 5p-2 = 0 \) sehingga \( p = \frac{2}{5} \)
  • Pembuat nol penyebut: \( (p-2)(p+2) = 0 \) sehingga \( p = 2 \) dan \( p = -2 \).

Selanjutnya, gambarkan nilai-nilai \(x\) pembuat nol pada garis bilangan, lalu lakukan uji titik pada tiap-tiap interval bilangan. Kita peroleh berikut:

pertidaksamaan pecahan

Lalu dengan memperhatikan syarat pertama yaitu \( p \neq 2 \) dan \( p \neq -2 \) maka himpunan penyelesaian yang memenuhi adalah \( p < -2 \) atau \( \frac{2}{5} \leq p < 2 \).

Jawaban C.

Contoh 6: UM UGM 2014

Nilai \(x\) yang memenuhi pertidaksamaan \( \frac{x^2-2x-3}{x-2} < x + 5 \) adalah…

  1. \( x < 2 \)
  2. \( x > \frac{7}{5} \)
  3. \( \frac{7}{5} < x < 2 \)
  4. \( -\frac{13}{5} < x < 2 \)
  5. \( x < \frac{7}{5} \) atau \( x > 2 \)
Pembahasan »

Lakukan operasi aljabar untuk membuat ruas kanan pertidaksamaan menjadi nol.

\begin{aligned} \frac{x^2-2x-3}{x-2} &< x + 5 \\[8pt] \frac{x^2-2x-3}{x-2}-(x+5) &< 0 \\[8pt] \frac{x^2-2x-3}{x-2}-\frac{(x+5)(x-2)}{x-2} &< 0 \\[8pt] \frac{x^2-2x-3}{x-2}-\frac{x^2+3x-10}{x-2} &< 0 \\[8pt] \frac{-5x+7}{x-2} &< 0 \\[8pt] \frac{5x-7}{x-2} &> 0 \end{aligned}

Syarat pertama dari pertidaksamaan di atas adalah \( x-2 \neq 0 \) sehingga diperoleh \( x \neq 2 \).

Berikutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:

  • Pembuat nol pembilang: \( 5x-7 = 0 \) maka \( x = \frac{7}{5} \).
  • Pembuat nol penyebut: \( x - 2 = 0 \) maka \(x = 2\).

Selanjutnya, gambarkan nilai-nilai \(x\) pembuat nol pada garis bilangan, lalu lakukan uji nilai \(x\) pada tiap-tiap interval bilangan. Kita peroleh berikut:

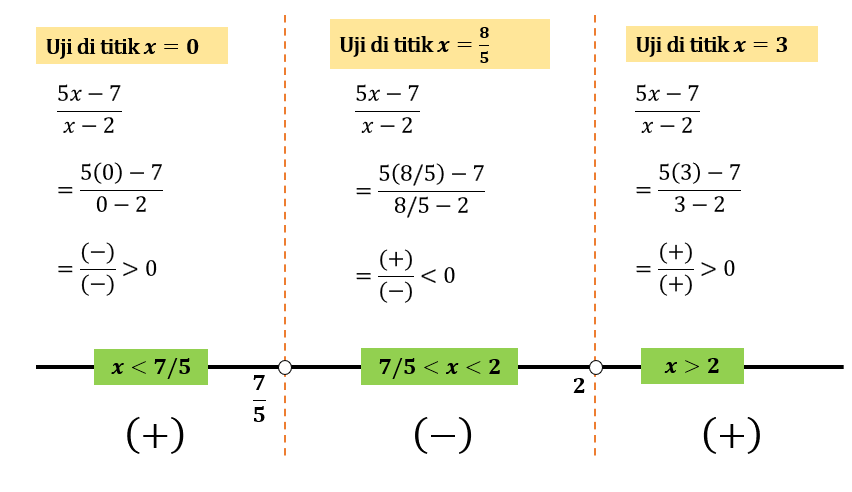
pertidaksamaan pecahan

Dari gambar dapat kita ambil kesimpulan bahwa daerah \( x < \frac{7}{5} \) atau \(x > 2\) merupakan himpunan penyelesaian pertidaksamaan soal karena pada daerah ini \( \frac{5x-7}{x-2} > 0 \).

Jawaban E.

Contoh 7: UMB-PT 2014

Solusi pertidaksamaan \( \frac{x^2-x-2}{-x^2+x-1} \leq 0 \) adalah himpunan semua bilangan real \(x\) yang memenuhi…

  1. \( x \leq -2 \) atau \(x \geq 1\)
  2. \( x \leq -1 \) atau \( x \geq 2\)
  3. \( -2 \leq x \leq 1 \)
  4. \( -1 \leq x \leq 2 \)
  5. \( x \leq 1 \)
Pembahasan »

Syarat sebuah pecahan mempunyai nilai adalah penyebut tidak boleh sama dengan nol atau \( -x^2+x-1 \neq 0 \).

\( -x^2+x-1 \) adalah definit negatif (selalu bernilai negatif untuk \(x\) bilangan real) karena \(a < 0\) dan \( D=b^2-4ac = 1-4(-1)(-1) = -3 (D<0) \).

Berikutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:

  • Pembuat nol pembilang yaitu:
    • \begin{aligned} x^2-x-2 &= 0 \\[8pt] (x-2)(x+1) &= 0 \\[8pt] x = 2 \ \text{atau} \ &x = -1 \end{aligned}
  • Pembuat nol penyebut: tidak ada.

Selanjutnya, gambarkan nilai-nilai \(x\) pembuat nol pada garis bilangan, kemudian lakukan uji titik \(x\) pada tiap-tiap interval. Kita peroleh berikut:

pertidaksamaan pecahan

Dari gambar dapat kita ambil kesimpulan bahwa daerah \(x \leq -1\) atau \(x \geq 2\) merupakan himpunan penyelesaian soal karena pada daerah ini \( \frac{(x-2)(x+1)}{x^2-x+1} \geq 0 \).

Jawaban B.

Contoh 8: SBMPTN 2015

Himpunan penyelesaian pertidaksamaan \( \frac{x-1}{x+1} < 1 \) adalah…

  1. \( \{ x \in R | x > 0 \} \)
  2. \( \{ x \in R | x > -1 \} \)
  3. \( \{ x \in R | x < -1 \} \)
  4. \( \{ x \in R | x < -1 \ \text{atau} \ x > 0 \} \)
  5. \( \{ x \in R | x < 0 \ \text{atau} \ x > 1 \} \)
Pembahasan »

Lakukan operasi aljabar untuk membuat ruas kanan pertidaksamaan menjadi nol:

\begin{aligned} \frac{x-1}{x+1} &< 1 \\[8pt] \frac{x-1}{x+1}-1 &< 0 \\[8pt] \frac{x-1}{x+1}-\frac{x+1}{x+1} &< 0 \\[8pt] \frac{x-1-x-1}{x+1} &< 0 \\[8pt] \frac{-2}{x+1} &< 0 \end{aligned}

Syarat pertama dari pertidaksamaan di atas adalah \( x + 1 \neq 0 \) sehingga \( x \neq -1 \).

Berikutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:

  • Pembuat nol pembilang: tidak ada
  • Pembuat nol penyebut: \( x + 1 = 0 \) maka \( x = -1 \).

Gambarkan nilai-nilai \(x\) pembuat nol pada garis bilangan dan lakukan uji titik \(x\) pada tiap-tiap interval bilangan. Kita peroleh berikut:

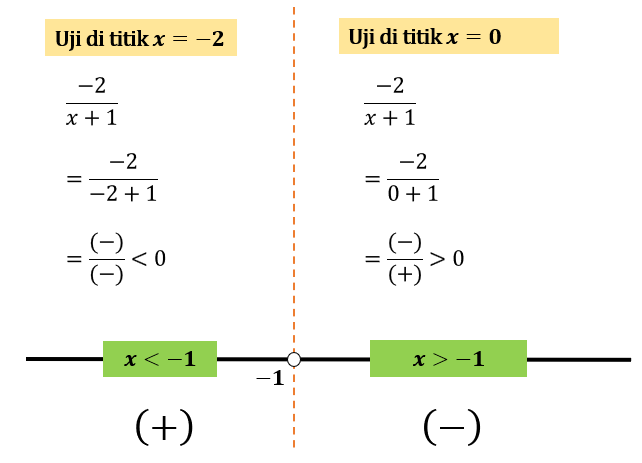
pertidaksamaan pecahan

Dari gambar bisa diambil kesimpulan bahwa daerah \( x > -1 \) merupakan himpunan penyelesaian soal karena pada daerah ini \( \frac{-2}{x+1} < 0 \).

Jawaban B.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel Terkait
img

Pertidaksamaan matematika: Rumus, contoh soal dan pembahasan

img

Pertidaksamaan hasil bagi: Rumus, contoh soal dan pembahasan


I was angered, for I had no shoes. Then I met a man who had no feet.

Chinese Proverb