www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Cara Menentukan Persamaan Garis Lurus
Cara Menentukan Persamaan Garis Lurus
Garis merupakan suatu objek matematika yang memegang peranan penting dalam teori geometri dan matematika pada umumnya. Terdapat dua cara untuk menyatakan persamaan garis lurus yakni secara eksplisit dan implisit.
Garis merupakan suatu objek matematika yang memegang peranan penting dalam teori geometri dan matematika pada umumnya. Bentuk umum dari persamaan garis lurus dapat dinyatakan dalam persamaan berikut

di mana \(m\) adalah kemiringan garis atau gradien, \(x\) adalah sebuah variabel berpangkat satu, dan \(n\) adalah sebuah konstanta. Persamaan garis lurus yang dinyatakan di atas disebut persamaan garis lurus eksplisit. Kita juga dapat menyatakan suatu persamaan garis lurus secara implisit, yakni dalam persamaan berikut
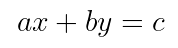
Untuk persamaan garis lurus, perhatikan gambar 1 berikut.

Gambar 1. Persamaan garis lurus
Ada beberapa cara menentukan garis lurus. Kita akan membahasnya satu per satu berikut ini.
Garis melalui titik pangkal (0,0) dengan gradien \(m\)
Jika diketahui garis melalui titik pangkal (0,0) dengan gradien \(m\) maka persamaan garisnya (Gambar 2) dapat ditentukan dengan rumus berikut
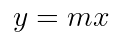
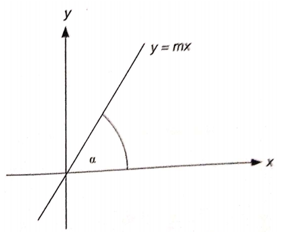
Gambar 2. Persamaan garis lurus
Contoh 1:
Tentukanlah persamaan garis lurus yang melewati titik pusat (0,0) dengan gradien 3.
Pembahasan:
Rumus untuk persamaan garis lurusnya adalah
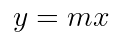
Dengan demikian, persamaan garis lurusnya adalah
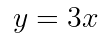
Garis melalui titik \(P(x_1, y_1)\) dengan gradien \(m\)
Jika diketahui garis melalui titik \(P(x_1, y_1)\) dengan gradien \(m\), maka persamaan garisnya (Gambar 3) adalah
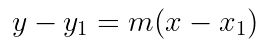

Gambar 3. Persamaan garis lurus
Contoh 2:
Tentukan persamaan garis lurus yang bergradien 3 dan melalui titik (-2,-3)!
Pembahasan:
Diketahui \(m = 3\) dan \((x_1, x_2) = (-2,3)\). Dengan demikian, kita peroleh

Jadi, persamaan garis lurusnya adalah \(y = 3x + 3\).
Garis melalui dua titik \((x_1,y_1)\) dan \((x_2,y_2)\)
Jika diketahui garis melalui dua titik \((x_1,y_1)\) dan \((x_2,y_2)\), maka gradien garisnya (Gambar 4) adalah

Jika rumus tersebut disubstitusikan ke dalam persamaan \(y-y_1=m(x-x_1)\) maka didapatkan persamaan garis lurus sebagai berikut.
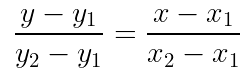

Gambar 4. Persamaan garis lurus
Contoh 3:
Tentukan persamaan garis lurus yang melalui titik (4,5) dan (-5,3).
Pembahasan:
Diketahui \( (x_1,y_1) = (4,5) \) dan \((x_2,y_2) = (-5,3)\).
Dengan demikian, persamaan garisnya adalah

Garis memotong sumbu \(x\) di titik \((a,0)\) dan memotong sumbu \(y\) di titik \((0,b)\)
Jika diketahui garis memotong sumbu \(x\) di titik \((a,0)\) dan memotong sumbu \(y\) di titik \((0,b)\), maka persamaan garisnya (Gambar 5) adalah


Gambar 5. Persamaan garis lurus
Contoh 4:
Tentukanlah persamaan garis lurus yang memotong sumbu \(x\) di titik (3,0) dan memotong sumbu \(y\) di titik (0,5).
Pembahasan:
Karena memotong sumbu \(x\) di (3,0), maka \(a = 3\) dan karena memotong sumbu \(y\) di (0,5) maka \(b = 5\). Dengan demikian, kita peroleh

Garis hanya melalui titik \((a,0)\) dan sejajar sumbu \(y\)
Jika diketahui garis hanya melalui titik \((a,0)\) dan sejajar sumbu \(y\), maka persamaan garisnya (Gambar 6) adalah: \[ x=a \]
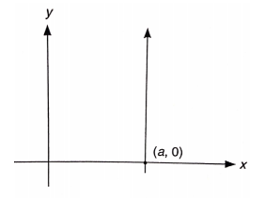
Gambar b. Persamaan garis lurus
Contoh 5:
Tentukan persamaan garis lurus yang melalui titik (4,0) dan sejajar sumbu \(y\).
Pembahasan:
Karena garis melalui titik (4,0), maka a = 4 sehingga persamaan garis lurusnya adalah
\[ x = 4 \]
Garis hanya melalui titik \((0,b)\) dan sejajar sumbu \(y\)
Jika diketahui garis hanya melalui titik \((0,b)\) dan sejajar sumbu \(x\), maka persamaan garisnya adalah: \[ y=b \]

Gambar 7. Persamaan garis lurus
Contoh 6:
Tentukan persamaan garis lurus yang melalui titik (0,5) dan sejajar sumbu \(x\).
Pembahasan:
Karena garis melalui titik (0,5) maka b = 5 sehingga persamaan garis lurusnya adalah
\[ y = 5 \]
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Goodbyes are only for those who love with their eyes. Because for those who love with heart and soul there is no such thing as separation.
