www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Persamaan Polinomial › Rumus ABC untuk Mencari Akar-akar Persamaan Kuadrat
Rumus ABC untuk Mencari Akar-akar Persamaan Kuadrat
Pada umumnya, suatu persamaan kuadrat atau persamaan polinomial (suku banyak) dengan pangkat tertinggi 2, dapat dituliskan sebagai

Penyelesaian atau pemecahan suatu persamaan kuadrat disebut sebagai akar-akar persamaan kuadrat tersebut. Yang dimaksud dengan akar-akar persamaan kuadrat adalah nilai dari variabel \(x\) yang memenuhi ketika disubstitusikan ke dalam persamaan tersebut.
Sebagai contoh, diketahui persamaan kuadrat \( x^2-5x+6 = 0 \). Akar-akar persamaan kuadrat ini yaitu \(x_1 = 2\) dan \(x_2 = 3\). Mengapa? Karena jika nilai-nilai ini disubstitusi ke dalam persamaan kuadrat tersebut, maka ruas kiri dan ruas kanan persamaan akan mempunyai nilai sama yakni bernilai nol.
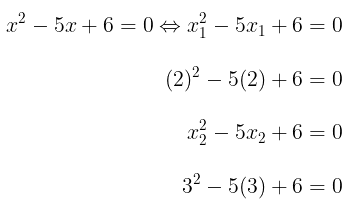
Terdapat beberapa cara untuk mencari akar-akar persamaan kuadrat, yaitu cara pemfaktoran, melangkapkan kuadrat sempurna, dan rumus abc. Pada artikel ini kita akan fokus pada metode ketiga ini yaitu rumus abc. Nilai a, b, dan c pada rumus abc mewakili koefisien-koefisien dari suatu persamaan kuadrat.
Berdasarkan rumus abc, akar-akar persamaan kuadrat dapat dicari dengan formula berikut.

Dengan demikian, akar-akarnya adalah

Bukti:

Contoh 1:
Persamaan kuadrat dari \(x^2-4x-6=0\) mempunyai akar-akar \(m\) dan \(n\) dengan ketentuan \(m < n\). Tentukan nilai dari \(n – m\).
Pembahasan:
Dari persamaan kuadrat \(x^2-4x-6=0\), kita peroleh a = 1, b = -4, dan c = -6. Dengan demikian, kita peroleh

Jadi, nilai \((n-m)\) adalah

Contoh 2:
Tentukanlah akar-akar persamaan kuadrat \(x^2+8x+12=0\).
Pembahasan:
Pada persamaan kuadrat di atas, nilai \(a=1, \ b=8\), dan \(c=12\). Berdasarkan rumus abc, diperoleh

Dengan demikian,

Jenis Akar-akar Persamaan Kuadrat
Jenis akar-akar persamaan kuadrat dapat ditentukan berdasarkan nilai “Diskriminan” (D). Nilai diskriminan dapat dicari dari rumus berikut
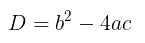
Sehingga rumus abc menjadi:

Berikut adalah jenis akar-akar berdasarkan diskriminannya:
- Jika \(D < 0\) maka akar-akarnya tidak real
- Jika \(D > 0\) maka akar-akarnya real \((x_1,x_2∈R)\) dan berbeda yakni \(x_1≠x_2\).
- Jika \(D = 0\) maka akar-akarnya real \((x_1,x_2∈R)\) dan sama atau kembar yakni \(x_1=x_2\).
Contoh 3:
Tanpa harus menyelesaikan persamaan kuadrat terlebih dahulu, tentukanlah jenis akar-akar persamaan kuadrat berikut.
- \( x^2 - 10x + 16 = 0 \)
- \( -2x + 3x - 6 = 0 \)
Pembahasan:
- Untuk \( x^2 - 10x + 16 = 0 \), maka \( a = 1, \ b = -10 \), dan \( c = 16 \). Dengan demikian, diskrimannya adalah
- Untuk \( -2x + 3x - 6 = 0 \), maka \( a = -2, \ b = 3 \), dan \( c = -6 \). Dengan demikian, diskrimannya adalah

Karena \(D = 36 > 0\), maka persamaan kuadrat \( x^2 - 10x + 16 = 0 \) mempunyai dua akar real yang berlainan dan rasional.

Karena \(D = -39 < 0\), maka persamaan kuadrat \( -2x + 3x - 6 = 0 \) tidak mempunyai akar real atau kedua akarnya tidak real atau imaginer.
Contoh 4:
Tentukanlah nilai p agar persamaan kuadrat \( 2x^2 - 4x + p = 0 \) mempunyai dua akar yang sama atau kembar.
Pembahasan:
Untuk \( 2x^2 - 4x + p = 0 \) maka \( a = 2, \ b = -4 \), dan \( c = p\). Dengan demikian, diskrimannya adalah

Agar mempunyai dua akar yang kembar, maka D harus bernilai 0 sehingga

Jadi, persamaan kuadrat \( 2x^2 - 4x + p = 0 \) akan mempunyai dua akar kembar jika \(p = 2\).
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Better to light one small candle than to curse the darkness.
