www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Sistem Persamaan Linear › Menyelesaikan Sistem Persamaan Linear Tiga Variabel
Menyelesaikan Sistem Persamaan Linear Tiga Variabel
Sistem persamaan linear tiga variabel (SPLTV) adalah sistem persamaan yang terdiri dari tiga persamaan di mana masing-masing persamaan memiliki tiga variabel. Kita dapat menyelesaikan SPLTV dengan dua cara yakni cara substitusi dan eliminasi.
Sistem persamaan linear tiga variabel adalah sistem persamaan yang terdiri dari tiga persamaan di mana masing-masing persamaan memiliki tiga variabel.
Sama halnya pada sistem persamaan linear dua variabel (SPLDV), kita dapat menyelesaikan atau mencari himpunan penyelesaian dari sistem persamaan linear tiga variabel (SPLTV) dengan dua cara atau metode, yakni metode substitusi dan metode eliminasi.
Metode Substitusi
Berikut adalah langkah-langkah untuk menerapkan metode substitusi pada sistem persamaan linear tiga variabel (SPLTV):
- Ubah salah satu persamaan pada sistem persamaan dan nyatakan \(x\) sebagai fungsi dari \(y\) dan \(z\), atau \(y\) sebagai fungsi dari \(x\) dan \(z\), atau \(z\) sebagai fungsi dari \(x\) dan \(y\).
- Substitusi fungsi \(x\) atau \(y\) atau \(z\) dari Langkah 1 pada dua persamaan lain sehingga diperoleh sistem persamaan linear dua variabel (SPLDV).
- Selesaikan sistem persamaan linear dua variabel (SPLDV) tersebut. Kita telah membahas penyelesaian SPLDV, sehingga tidak akan dijelaskan lagi di sini.
Contoh 1:
Tentukan nilai \(x\), \(y\) dan \(z\) dari sistem persamaan linear tiga variabel berikut.

Pembahasan:
Kita akan menggunakan metode substitusi dengan mengikuti langkah-langkah yang dijelaskan di atas.
Langkah 1: Ubah persamaan pertama (anda bebas mengubah persamaan manapun) sehingga diperoleh \(z\) sebagai fungsi dari \(x\) dan \(y\), yakni

Langkah 2: Substitusi persamaan (iv) ke persamaan lain yakni persamaan dua dan tiga, lalu lakukan penyederhanaan. Kita peroleh


Perhatikan bahwa kita telah memperoleh nilai \(x\) dan \(y\), yakni \(x = -5\) dan \(y = -3\). Dengan mensubstitusi nilai \(x\) dan \(y\) pada persamaan (iv), kita peroleh nilai \(z\) yakni

Jadi, nilai \(x, y\) dan \(z\) yang memenuhi sistem persamaan linear tiga variabel tersebut adalah \(x = -5, \ y = -3, \ z = 2\) atau kita nyatakan dengan \((x,y,z)= (-5,-3,2)\).
Perhatikan bahwa dari Contoh 1, kita hanya menggunakan dua langkah dan berhasil mendapatkan nilai \(x\) dan \(y\) sehingga kita tidak memerlukan langkah 3. Ini hanya kebetulan saja. Sering kali, kita harus menggunakan langkah ketiga. Oleh karena itu, kita akan memberikan satu Contoh lagi.
Contoh 2:
Carilah himpunan penyelesaian dari sistem persamaan linear tiga variabel (SPLTV) berikut ini dengan metode substitusi.

Pembahasan:
Pertama, kita tentukan dulu persamaan yang paling sederhana dari ketiga persamaan yang ada. Dalam hal ini, persamaan pertama tampak lebih sederhana sehingga kita ubah persamaan pertama dan diperoleh \(x\) sebagai fungsi dari \(y\) dan \(z\).
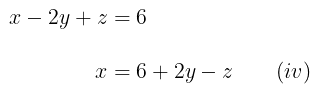
Substitusi variabel \(x\) dalam persamaan (iv) ke persamaan 2. Kita peroleh
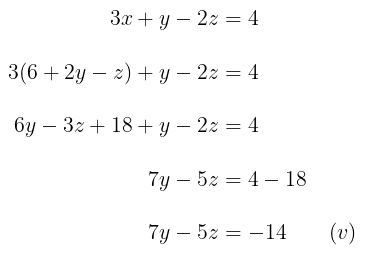
Substitusi variabel \(x\) dalam persamaan (iv) ke persamaan 3. Kita peroleh
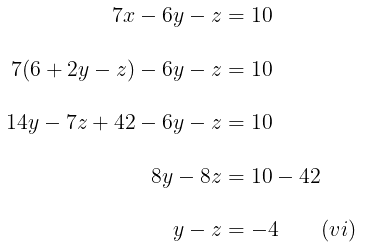
Persamaan (v) dan (vi) membentuk sistem persamaan linear dua variabel (SPLDV) dalam variabel \(y\) dan \(z\), yakni
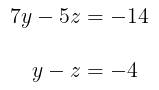
Kita akan menyelesaikan SPLDV ini, sehingga diperoleh nilai untuk variabel \(y\) dan \(z\). Dari persamaan (vi), kita peroleh

Substitusi variabel \(y\) ke dalam persamaan persamaan (v), sehingga diperoleh

Substitusi nilai \(z = 7\) yang kita peroleh di atas ke salah satu persamaan SPLDV, misalnya \(y - z = -4\). Kita peroleh

Terakhir, substitusi nilai \(y = 3\) dan \(z = 7\) ke salah satu dari SPLTV, misalnya \( x-2y + z = 6 \) sehingga kita peroleh

Jadi, nilai \(x, y\) dan \(z\) yang memenuhi SPLTV tersebut adalah \((x,y,z) = (5, 3, 7)\).
Metode Eliminasi
Berikut adalah langkah-langkah yang diperlukan untuk menerapkan metode eliminasi:
- Ambil sembarang dua persamaan dari tiga persamaan yang ada (misal persamaan 1 dan 2, atau persamaan 1 dan 3 atau persamaan 2 dan 3). Lalu, menyamakan salah satu koefisien dari variabel \(x\) atau \(y\) atau \(z\) dari kedua persamaan yang diambil dengan cara mengalikan konstanta yang sesuai. Setelah itu, eliminasi atau hilangkan variabel yang memiliki koefisien yang sama dengan cara menambahkan atau mengurangkan kedua persamaan sehingga diperoleh persamaan baru dengan dua variabel.
- Lakukan hal yang sama seperti Langkah 1 pada pasangan persamaan lain.
- Dari Langkah 1 dan 2, kita peroleh sistem persamaan linear dua variabel. Lalu, selesaikan SPLDV tersebut.
- Tuliskan penyelesaiannya dalam \((x,y,z)\).
Contoh 3:
Carilah nilai \(x, y\) dan \(z\) yang memenuhi sistem persamaan linear tiga variabel berikut:

Pembahasan:
Kita akan menggunakan metode eliminasi dengan mengikuti langkah-langkah yang dijelaskan di atas.
Langkah 1: Ambil dua persamaan yakni persamaan 1 dan 2. Karena koefisien variabel \(z\) adalah sama, maka kita akan eliminasi variabel \(z\) dengan cara menambahkan kedua persamaan tersebut sehingga diperoleh persamaan baru dengan dua variabel yakni \(x\) dan \(y\).

Langkah 2: Ulangi Langkah 1 pada pasangan persamaan lain. Kita ambil pasangan persamaan 2 dan 3. Kita perlu eliminasi variabel z dengan cara mengalikan persamaan 2 dengan nilai 2 dan persamaan tiga dengan nilai 1, yakni

Langkah 3: Dari Langkah 2, kita peroleh nilai \(x = 5\). Dengan substitusi nilai \(x\) ke persamaan (iv) kita peroleh nilai \(y\), yakni

Substitusi nilai \(x\) dan \(y\) pada persamaan 2 (anda bebas memilih salah satu dari tiga persamaan yang diberikan pada soal). Kita peroleh

Langkah 4: Jadi, penyelesaian dari sistem persamaan linear tiga variabel tersebut adalah \((x,y,z) = (5, 3, -1)\).
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Segala sesuatunya menjadi baik bagi orang yang berusaha sebaik-baiknya mengusahakan segala sesuatu.
