Barisan dan deret aritmatika: Rumus, contoh soal dan pembahasan

Matematika Dasar » Barisan dan Deret › Barisan dan deret aritmatika: Rumus, contoh soal dan pembahasan

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Barisan dan deret aritmatika: Rumus, contoh soal dan pembahasan

Barisan aritmatika adalah suatu barisan yang tersusun dengan suatu pola yang teratur yakni setiap suku berikutnya setelah suku pertama merupakan penjumlahan atau pengurangan dari suku sebelumnya dengan suatu nilai tertentu yang tetap.

Barisan merupakan urutan dari suatu bilangan berdasarkan aturan atau pola tertentu. Sama seperti himpunan, suatu barisan juga mempunyai anggota (elemen) yang biasanya disebut suku. Perhatikan contoh barisan yang terdiri dari 10 suku berikut.

Suku pertama dari barisan tersebut adalah 2 dan suku kedua yaitu 5 dan demikian seterusnya hingga suku terakhirnya adalah 29. Suku pertama suatu barisan sering dinotasikan dengan \(a\) atau \(U_1\) sedangkan suku ke-n dari suatu barisan dinyatakan dengan \(U_n\).

Perhatikan kembali barisan yang diberikan di atas. Anda bisa melihat bahwa barisan tersebut tersusun dengan suatu pola yang teratur, yakni setiap suku berikutnya setelah suku pertama merupakan penjumlahan dari suku sebelumnya dengan suatu nilai tertentu yang tetap yakni 3. Nilai tertentu yang tetap tersebut sering dinotasikan dengan huruf \(b\). Barisan yang demikian, kita sebut barisan aritmetika dan penjumlahan dari suku-suku suatu barisan aritmetika disebut deret aritmetika.

Jadi, barisan aritmetika adalah suatu barisan yang tersusun dengan suatu pola yang teratur yakni setiap suku berikutnya setelah suku pertama merupakan penjumlahan atau pengurangan dari suku sebelumnya dengan suatu nilai tertentu yang tetap.

Rumus suku ke-\(n\) barisan aritmetika

Karena selisih antara suku-suku yang berdekatan dalam barisan aritmetika selalu sama yaitu \(b\), maka dalam barisan aritmatika kita peroleh persamaan:

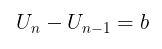
Sebagai contoh, dari barisan yang diberikan di awal artikel, kita peroleh nilai \(b\), yaitu:

Jika diketahui suku ke-\(k\) dan selisih antar suku yang berdekatan adalah \(b\), maka nilai suku ke-\(n\) dari suatu barisan aritmatika dapat diperoleh dengan persamaan berikut:

Jika yang diketahui adalah suku pertama \((a = U_k = U_1, k=1)\) dan selisih antara sukunya adalah \(b\), maka nilai \(U_n\) menjadi

Rumus suku tengah barisan aritmetika

Terkadang dalam soal aritmetika akan dijumpai permasalahan mencari suku tengah. Rumus untuk mencari suku tengah barisan aritmetika, yaitu:

\begin{aligned} U_t &= \frac{a+U_n}{2} \ \text{atau} \ U_t = \frac{U_1+U_n}{2} \\[8pt] t &= \frac{n+1}{2} \end{aligned}

Keterangan: \( U_t \) adalah suku tengah barisan aritmetika.

Rumus jumlah \(n\) suku pertama barisan aritmetika

Deret aritmatika merupakan penjumlahan dari suku-suku barisan aritmatika. Penjumlahan suku pertama hingga suku ke-\(n\) barisan aritmatika diberikan oleh:

atau dapat dituliskan juga sebagai:

Jika hanya diketahui nilai suku pertama (\(a\)) dan nilai suku ke-\(n\), maka rumus deret aritmatikanya menjadi:

Karena rumus suku ke-\(n\) yaitu \( U_n = a+(n-1)b \), maka dari \( S_n = \frac{n}{2} (a+U_n) \), diperoleh:

\begin{aligned} S_n &= \frac{n}{2} (a+U_n) \\[8pt] &= \frac{n}{2}(a+(a+(n-1)b)) \\[8pt] &= \frac{n}{2}(2a+(n-1)b) \end{aligned}

Sekarang perhatikan bahwa kita dapat mencari jumlah deret hingga suku ke-\((n-1)\), yakni:

Jika kita kurangkan \( S_n \) dengan \( S_{n-1} \), maka kita peroleh persamaan untuk \( U_n \), yaitu:

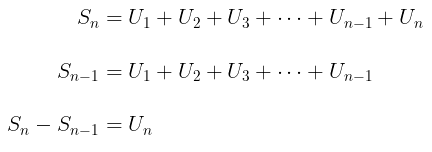
Jadi, kita peroleh rumus suku ke-\(n\):

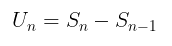
Rumus sisipan barisan aritmetika

Sisipan pada barisan aritmetika adalah menambahkan beberapa buah bilangan di antara dua suku yang berurutan pada suatu deret aritmetika sehingga terbentuk barisan aritmetika yang baru. Beda (\(b\)) pada barisan aritmetika yang baru, yaitu:

\[ b' = \frac{b}{k+1} \]

Keterangan: \(b'\) = beda dari barisan aritmetika yang baru; \(b\) = beda dari barisan aritmetika yang sebelumnya; \(k\) = banyak bilangan yang disisipkan.

Contoh soal dan pembahasan barisan dan deret aritmetika

Setelah memahami pengertian barisan dan deret aritmetika di atas beserta rumus-rumusnya, berikut ini kita akan membahas beberapa contoh soal terkait barisan dan deret aritmetika.

Contoh 1:

Misalkan diketahui nilai dari suku ke-16 pada suatu deret aritmatika adalah 34 dengan bedanya yaitu 3. Hitunglah suku pertama barisan tersebut.

Pembahasan »

Dari soal diketahui \( U_{16} = 34, \ n = 16, \ b = 3 \). Dengan demikian, suku pertama dari barisan tersebut adalah

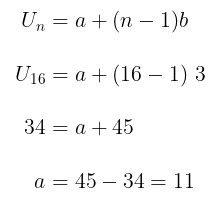
Jawaban A.

Contoh 2:

Suatu deret aritmatika memiliki suku ke-5 sama dengan 42, dan suku ke-8 sama dengan 15. Jumlah 12 suku pertama deret tersebut adalah...

-21
21
342
-342
0

Pembahasan »

Diketahui bahwa \(U_n = 42, U_8 = 15\), maka dapat digunakan rumus:

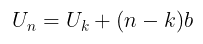
Dengan demikian,

Sehingga, kita peroleh

Selanjutnya, carilah suku ke-12 deret tersebut, yakni

Jadi, jumlah 12 suku pertama deret tersebut adalah

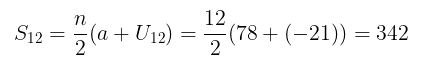
Jawaban C.

Contoh 3:

Diketahui barisan aritmetika \( 15, 18, 21, \cdots, 231 \). Tentukan nilai suku tengahnya dan merupakan suku keberapa.

Nilai suku tengah 123 pada suku ke-37
Nilai suku tengah 132 pada suku ke-37
Nilai suku tengah 133 pada suku ke-37
Nilai suku tengah 143 pada suku ke-37
Nilai suku tengah 153 pada suku ke-37

Pembahasan »

Diketahui \(a = 15, b = 3, \) dan \(U_n = 231\) sehingga diperoleh:

\begin{aligned} U_t &= \frac{1}{2}(a+U_n) = \frac{1}{2}(15+231) \\[8pt] &= \frac{1}{2}(246) = 123 \\[8pt] U_n &= a+(n-1)b \\[8pt] U_t &= a+(t-1)b \\[8pt] 123 &= 15+(t-1) \cdot 3 \\[8pt] 123 &= 15+3t-3 \\[8pt] 123 &= 3t+12 \\[8pt] 3t &= 111 \\[8pt] t &= \frac{111}{3} = 37 \end{aligned}

Jadi, suku tengah barisan aritmetika tersebut adalah 123 dan berada pada suku ke-37.

Jawaban A.

Contoh 4: UN 2012

Seorang penjual daging pada bulan Januari dapat menjual 120 kg, bulan Februari 130 kg, Maret dan seterusnya selama 10 bulan selalu bertambah 10 kg dari bulan sebelumnya. Jumlah daging yang terjual selama 10 bulan adalah…

1.050 kg
1.200 kg
1.350 kg
1.650 kg
1.750 kg

Pembahasan »

Kita dapat menyelesaikan soal ini menggunakan konsep deret aritmetika dengan suku pertama 120 dan beda 10. Jumlah daging yang terjual selama 10 bulan sama dengan jumlah 10 suku pertama deret tersebut sehingga kita peroleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1) \cdot b) \\[8pt] S_{10} &= \frac{10}{2}(2(120)+(10-1) \cdot 10) \\[8pt] &= 5(240+9 \cdot 10) \\[8pt] &= 5 (240+90) \\[8pt] &= 5(330) \\[8pt] &= 1650 \end{aligned}

Jadi, jumlah daging yang terjual selama 10 bulan adalah 1.650 kg.

Jawaban D.

Contoh 5: SNMPTN 2012

ika suku pertama barisan aritmetika adalah -2 dengan beda 3, \(S_n\) adalah jumlah \(n\) suku pertama deret aritmetika tersebut, dan \( S_{n+2}-S_n = 65 \), maka nilai \(n\) adalah…

Pembahasan »

Diketahui \(a = -2\) dan \(b=3\) sehingga kita peroleh berikut:

\begin{aligned} S_{n+2}-S_n &= 65 \\[8pt] \frac{n+2}{2} \left( 2a+((n+2)-1) \cdot b \right)-\frac{n}{2} \left( 2a+(n-1) \cdot b \right) &= 65 \\[8pt] \frac{n+2}{2} \left( 2a+(n+1) \cdot b \right)-\frac{n}{2} \left( 2a+(n-1) \cdot b \right) &= 65 \\[8pt] \frac{n+2}{2} \left( 2(-2)+(n+1) \cdot 3 \right)-\frac{n}{2} \left( 2(-2)+(n-1) \cdot 3 \right) &= 65 \\[8pt] \frac{n+2}{2} \left( -4+3n+3 \right)-\frac{n}{2} \left( -4+3n-3 \right) &= 65 \\[8pt] (n+2) \left( 3n-1 \right)- n \left( 3n-7 \right) &= 130 \\[8pt] (3n^2-n+6n-2)-(3n^2-7n) &= 130 \\[8pt] 3n^2+5n-2-3n^2-3n^2+7n &= 130 \\[8pt] 12n-2 &= 130 \\[8pt] n = \frac{132}{12} &= 11 \end{aligned}

Jawaban A.

Contoh 6: UN 2013

Diketahui suku ke-3 dan suku ke-8 suatu barisan aritmatika berturut-turut adalah 2 dan -13. Jumlah 20 suku pertama deret tersebut adalah…

-580
-490
-440
-410
-380

Pembahasan »

Diketahui \( U_3 = a+2b =2 \) dan \( U_8 = a+7b=-13 \) sehingga diperoleh \(-5b=15\) atau \(b=-3\) dan \(a=8\). Dengan demikian, jumlah 20 suku pertama deret tersebut adalah…

\begin{aligned} S_n &= \frac{n}{2} (2a+(n-1) \cdot b) \\[8pt] S_{20} &= \frac{20}{2}(2 \cdot 8 + (20-1) \cdot (-3)) \\[8pt] &= 10(16+9(-3)) \\[8pt] &= 10(16-57) \\[8pt] &= 10(-41) \\[8pt] &= -410 \end{aligned}

Jawaban D.

Contoh 7: UN 2010

Diketahui barisan aritmatika dengan \( U_n \) adalah suku ke-n. Jika \( U_2 + U_{15} + U_{40} = 165 \) maka \( U_{19} = \cdots \)

10
19
28,5
55
82,5

Pembahasan »

Dari \( U_2 + U_{15} + U_{40} = 165 \), kita dapatkan hasil berikut:

\begin{aligned} U_2+U_{15}+U_{40} &= 165 \\[8pt] (a+b)+(a+14b)+(a+39b) &= 165 \\[8pt] 3a+54b &= 165 \\[8pt] 3(a+18b) &= 165 \\[8pt] a+18b &= 55 \\[8pt] U_{19} &= 55 \end{aligned}

Jawaban D.

Contoh 8: SBMPTN 2013

Diketahui a, b, dan c berturut-turut adalah suku ke-2, ke-4 dan ke-6 barisan aritmatika. Jika \( \frac{a+b+c}{b+1} = 4 \), maka nilai \(b\) adalah…

-4
-1
1
2
4

Pembahasan »

Karena merupakan barisan aritmatika, maka berlaku:

\begin{aligned} 2U_2 &= U_1 + U_3 \\[8pt] 2b &= a+c \\[8pt] \frac{a+b+c}{b+1} &= 4 \\[8pt] \frac{(a+c)+b}{b+1} &= 4 \\[8pt] \frac{2b+b}{b+1} &= 4 \\[8pt] 3b &= 4b+4 \\[8pt] b &= -4 \end{aligned}

Jawaban A.

Contoh 9: SBMPTN 2014

Jika \( a_1, a_2, a_3 \) adalah barisan aritmatika dan \(a_1, a_2, a_1+a_3\) adalah barisan geometri, maka \( \frac{a_3}{a_1} = \cdots \)

Pembahasan »

Dari barisan aritmatika \( a_1, a_2, a_3 \) diperoleh \( 2a_2 = a_1+a_3 \) dan dari barisan geometri \(a_1, a_2, a_1+a_3\), kita peroleh:

\begin{aligned} a_2^2 &= a_1 \cdot (a_1+a_3) \\[8pt] a_2^2 &= a_1 \cdot (2a_2) \\[8pt] a_2 &= 2a_1 \end{aligned}

Persamaan yang kita peroleh di atas kita substitusi ke persamaan \( 2a_2 = a_1+a_3 \) sehingga didapatkan hasil berikut:

\begin{aligned} 2a_2 &= a_1+a_3 \\[8pt] 2(2a_1) &= a_1+a_3 \\[8pt] 4a_1 &= a_1+a_3 \\[8pt] 3a_1 &= a_3 \\[8pt] \frac{a_3}{a_1} &= \frac{3}{1} = 3 \end{aligned}

Jawaban C.

Contoh 10: UM UGM 2014

Tiga bilangan membentuk barisan aritmatika. Jika jumlah suku ke-1 dan suku ke-3 adalah 30 dan jumlah dari logaritma suku ke-1, ke-2, dan ke-3 adalah \( 3+\log 3 \), maka suku ke-1 barisan tersebut adalah…

-5 atau 5
5 atau -10
5 atau 25
10 atau 20
25 atau 15

Pembahasan »

Misalkan tiga bilangan yang membentuk barisan aritmatika tersebut yaitu (a-b), a, dan (a+b). Karena diketahui jumlah suku ke-1 dan suku ke-3 adalah 30, maka diperoleh:

\begin{aligned} U_1 + U_3 &= 30 \\[8pt] (a-b)+(a+b) &= 30 \\[8pt] 2a &= 30 \\[8pt] a &= 15 \end{aligned}

Untuk \(a=15\) dan jumlah dari logaritma suku ke-1, ke-2 dan ke-3 adalah \( 3+\log 3 \), maka kita peroleh:

\begin{aligned} \log U_1 + \log U_2 + \log U_3 &= 3 + \log 3 \\[8pt] \log (a-b) + \log(a) + \log(a+b) &= \log 1000 + \log 3 \\[8pt] \log (a-b)(a)(a+b) &= \log (1000 \cdot 3) \\[8pt] \log(15-b)(15)(15+b) &= \log 3000 \\[8pt] (15-b)(15)(15+b) &= 3000 \\[8pt] (15-b)(15+b) &= 200 \\[8pt] 225-b^2 &= 200 \\[8pt] b^2 &= 225-200 = 25 \\[8pt] b &= \pm 5 \end{aligned}

Untuk \(b=5\) dan \(a=15\) maka barisan aritmatika tersebut adalah 10, 15, 20. Sedangkan untuk \(b=-5\) dan \(a=15\) maka barisan aritmatika tersebut adalah 20, 15, 10.

Jawaban D.

Contoh 11: UN 2000

Dari deret aritmetika diketahui suku tengah 32. Jika jumlah \(n\) suku pertama deret itu 672, banyak suku deret itu adalah…

Pembahasan »

Diketahui \( U_T = 32 \) dan \( S_n = 672 \) sehingga diperoleh:

\begin{aligned} U_T = 32 \Leftrightarrow U_T &= \frac{a+U_n}{2} = 32 \\[8pt] a+U_n &= 64 \\[8pt] S_n &= 672 \\[8pt] \frac{n}{2}(a+U_n) &= 672 \\[8pt] \frac{n}{2}(64) &= 672 \\[8pt] 32n &= 672 \\[8pt] n &= \frac{672}{32} = 21 \end{aligned}

Jawaban C.

Contoh 12:

Suku ke-\(n\) suatu deret aritmetika adalah \( U_n = 2n-3 \). Rumus jumlah \(n\) suku pertama adalah…

\( 2n-5 \)
\( n(n+1) \)
\( n(n-2) \)
\( \frac{1}{2}n-3 \)
\( \frac{1}{2}n+5 \)

Pembahasan »

Diketahui \( U_n = 2n-3 \) sehingga \(a = U_1 = 2(1)-3=-1\). Jumlah \(n\) suku pertama barisan aritmetika tersebut dapat dihitung sebagai berikut:

\begin{aligned} S_n &= \frac{n}{2}(a+U_n) \\[8pt] &= \frac{n}{2}(-1+2n-3) \\[8pt] &= \frac{n}{2}(2n-4) \\[8pt] &= n(n-2) \end{aligned}

Jawaban C.

Contoh 13:

Jika barisan aritmetika dengan \( U_1+U_7+U_{13} = 54 \), maka suku ke-7 barisan tersebut adalah…

Pembahasan »

Dari soal diketahui \( U_1+U_7+U_{13} = 54 \) sehingga:

\begin{aligned} U_1+U_7+U_{13} &= 54 \\[8pt] a+(a+6b)+(a+12b) &= 54 \\[8pt] 3a+18b &= 54 \\[8pt] 3(a+6b) &= 54 \\[8pt] a+6b &= 18 \\[8pt] U_7 = a+6b &= 18 \end{aligned}

Jawaban E.

Contoh 14:

Di antara bilangan 20 dan bilangan 35 disisipkan empat bilangan sehingga membentuk barisan aritmetika. Hitunglah beda dari barisan tersebut.

Pembahasan »

Dari soal diperoleh \(k = 4\) dan \( b = 35-20 = 15 \) sehingga beda barisan aritmetika tersebut yaitu:

\begin{aligned} b' &= \frac{b}{k+1} = \frac{15}{4+1} \\[8pt] &= \frac{15}{5}=3 \end{aligned}

Jadi, beda dari barisan aritmetika yang terbentuk adalah 3.

Jawaban B.

Contoh 15:

Diketahui suku pertama deret aritmetika adalah 15, bedanya 5 dan jumlah \(n\) suku pertama adalah 375. Tentukan banyaknya suku dari deret aritmetika tersebut.

Pembahasan »

Diketahui \(a = 15, b = 5,\) dan \(S_n = 375\). Dari rumus umum jumlah \(n\) suku pertama deret aritmetika, diperoleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] 375 &= \frac{n}{2} (2 \cdot 15 + (n-1) \cdot 5) \\[8pt] 375 &= \frac{n}{2} (30+5n-5) \\[8pt] 375 &= \frac{n}{2}(5n+25) \\[8pt] 750 &= 5n^2+25n \\[8pt] 0 &= 5n^2+25n-750 \\[8pt] 0 &= n^2+5n-150 \\[8pt] 0 &= (n-10)(n+15) \\[8pt] n &= 10 \ \text{atau} \ n = -15 \end{aligned}

Nilai \(n\) harus bernilai positif sehingga yang memenuhi adalah \(n=10\). Jadi, banyak suku deret aritmetika tersebut adalah 10.

Jawaban A.

Contoh 16:

Diketahui barisan aritmetika \( {}^2 \! \log \frac{5}{16}, {}^2 \! \log \frac{5}{8}, {}^2 \! \log \frac{5}{4}, \cdots \). Tentukanlah rumus suku ke-\(n\) dan suku ke-12.

Pembahasan »

Kita tentukan dulu beda dari barisan aritmetika tersebut, yakni:

\begin{aligned} b &= U_2 - U_1 = {}^2 \! \log \frac{5}{8} - {}^2 \! \log \frac{5}{16} \\[8pt] &= {}^2 \! \log \frac{\frac{5}{8}}{\frac{5}{16}} = {}^2 \! \log \left( \frac{5}{8} \times \frac{16}{5} \right) \\[8pt] &= {}^2 \! \log 2 = 1 \end{aligned}

Kita peroleh \( {}^2 \! \log \frac{5}{16} \) dan \(b = 1\) sehingga rumus suku ke-\(n\) dan suku ke-12 barisan aritmetika tersebut, yaitu:

\begin{aligned} U_n &= a+(n-1) \cdot b \\[8pt] &= {}^2 \! \log \frac{5}{16} + (n-1) \cdot 1 \\[8pt] &= {}^2 \! \log \frac{5}{16} + {}^2 \! \log 2^{(n-1)} \\[8pt] U_n &= {}^2 \! \log \left( \frac{5}{16} \cdot 2^{(n-1)} \right) \\[8pt] U_{12} &= {}^2 \! \log \left( \frac{5}{16} \cdot 2^{(12-1)} \right) \\[8pt] &= {}^2 \! \log \left( \frac{5}{2^4} \cdot 2^{11} \right) = {}^2 \! \log \left( 5 \cdot 2^7 \right) \\[8pt] &= {}^2 \! \log \left( 5 \cdot 128 \right) \\[8pt] &= {}^2 \! \log 640 \end{aligned}

Contoh 17: UNBK Matematika IPA 2018

Diketahui suatu barisan aritmatika dengan \( U_2 = 8 \) dan \( U_6 = 20 \). Jumlah 6 suku pertama barisan tersebut adalah…

Pembahasan »

Ingat bahwa untuk barisan dan deret aritmatika, kita mempunyai rumus berikut ini:

\begin{aligned} U_n &= a+(n-1) \cdot b \\[8pt] S_n &= \frac{n}{2}(2a+(n-1) \cdot b) \end{aligned}

Dari soal diketahui \( U_2 = 8 \) dan \(U_6 = 20\) sehingga diperoleh:

\begin{aligned} U_n &= a+(n-1) \cdot b \\[8pt] U_2 &= a + (2-1) \cdot b \\[8pt] 8 &= a + b \quad \cdots (1) \\[8pt] U_6 &= a+(6-1) \cdot b \\[8pt] 20 &= a+5b \quad \cdots (2) \end{aligned}

Dengan menyelesaikan persamaan (1) dan (2) di atas, diperoleh nilai \(a=5\) dan \(b=3\). Dengan demikian, diperoleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1) \cdot b) \\[8pt] S_6 &= \frac{6}{2}(2 \cdot 5+(6-1) \cdot 3) \\[8pt] &= 3 (10+5 \cdot 3) \\[8pt] &= 3 \cdot 25 \\[8pt] &= 75 \end{aligned}

Jadi, jumlah 6 suku pertama dari barisan aritmatika tersebut adalah 75.

Jawaban B.

Contoh 18:

Rumus umum dari barisan aritmatika \( -8,0,8,16, \cdots \) adalah…

\( U_n = 2n \)
\( U_n = 2n + 2 \)
\( U_n = 4n-6 \)
\( U_n = 8n+16 \)
\( U_n = 8n-16 \)

Pembahasan »

Dari soal diketahui \(a=-8\) dan \(b=9\). Dengan menggunakan formula suku ke-n barisan aritmatika, kita peroleh hasil berikut:

\begin{aligned} U_n &= a + (n-1) \cdot b \\[8pt] &= -8 + (n-1) \cdot 8 \\[8pt] &= -8+8n-8 \\[8pt] &= 8n-16 \end{aligned}

Jadi, rumus umum barisan tersebut adalah \( U_n = 8n-16 \).

Jawaban E.

Contoh 19:

Diketahui suatu barisan aritmatika dengan \( U_4 = 17 \) dan \( U_9 = 37 \). Suku ketujuh barisan tersebut adalah…

Pembahasan »

Ingat bahwa rumus untuk suku ke-n bariasan aritmatika adalah \( U_n = a+(n-1)b \). Untuk menyelesaikan soal ini, pertama kita cari dulu nilai \(b\) dan \(a\). Nilai \(b\) dapat diperoleh dengan rumus sebagai berikut:

\begin{aligned} b &= \frac{U_n-U_m}{n-m} = \frac{U_9-U_4}{9-4} \\[8pt] &= \frac{37-17}{9-4} = \frac{20}{5} \\[8pt] &= 4 \end{aligned}

Selanjutnya, akan dicari nilai \(a\) (suku pertama) menggunakan persamaan \( U_4 = 17 \), yakni:

\begin{aligned} U_n &= a + (n-1)b \\[8pt] U_4 &= a + (4-1) \cdot 4 \\[8pt] 17 &= a+12 \\[8pt] a &= 17-12 \\[8pt] &=5 \end{aligned}

Dengan demikian, suku ke-7 barisan tersebut, yaitu:

\begin{aligned} U_n &= a + (n-1)b \\[8pt] U_{7} &= 5 + (7-1) \cdot 4 \\[8pt] &= 5+ 6 \cdot 4 \\[8pt] &= 5+24 \\[8pt] &= 29 \end{aligned}

Jawaban B.

Contoh 20:

Di antara tiap dua suku bilangan 20, 68, dan 116 akan disisipkan 5 bilangan sehingga membentuk barisan aritmatika. Jumlah seluruh bilangan yang disisipkan adalah…

Pembahasan »

Barisan aritmatika yang dimaksud adalah \( 20, U_2, U_3, U_4, U_5, U_6, 68, U_8, U_9, U_{10}, U_{11}, U_{12}, 116 \). Dari sini diketahui \( U_1 = a = 20 \) dan karena \( U_7 = 68 \), maka

\begin{aligned} U_7 &= 68 \\[8pt] a + 6b &= 68 \\[8pt] 20 + 6b &= 68 \\[8pt] 6b &= 68-20 \\[8pt] b &= \frac{48}{6} = 8 \end{aligned}

Dari hasil di atas telah diperoleh nilai \(a = 20\) dan \(b=8\). Selanjutnya, akan dihitung jumlah 13 suku pertama barisan tersebut, yakni:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{13} &= \frac{13}{2} (2 \cdot 20 + (13-1) \cdot 8) \\[8pt] &= \frac{13}{2}(40+96) \\[8pt] &= \frac{13}{2}(136) = 884 \end{aligned}

Dengan demikian, jumlah semua bilangan yang disisipkan itu, yaitu:

\begin{aligned} &\Leftrightarrow S_{13}-U_1-U_7-U_{13} \\[8pt] &\Leftrightarrow 884-20-68-116 \\[8pt] &\Leftrightarrow 680 \end{aligned}

Jawaban A.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar » Barisan dan Deret › Barisan dan deret aritmatika: Rumus, contoh soal dan pembahasan