www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Turunan Fungsi › Garis Singgung pada Suatu Kurva
Garis Singgung pada Suatu Kurva
Pada artikel ini, kita akan membahas definisi umum garis singgung dan metode untuk menemukan kemiringan dan persamaannya menggunakan konsep turunan.
Studi mengenai turunan terkait erat dengan konsep geometri untuk garis singgung suatu kurva. Oleh karena itu, kita akan membahas definisi umum garis singgung dan metode untuk menemukan kemiringan dan persamaannya menggunakan konsep turunan.
Perhatikan grafik dari persamaan \(y=f(x)\) pada Gambar 1. Titik \(P\) mempunyai koordinat \((c,f(c))\), titik \(Q\) di dekatnya mempunyai koordinat \((c+h,f(c+h))\), dan talibusur yang melalui \(P\) dan \(Q\) mempunyai kemiringan \(m_{sec}\) yang diberikan oleh
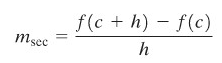
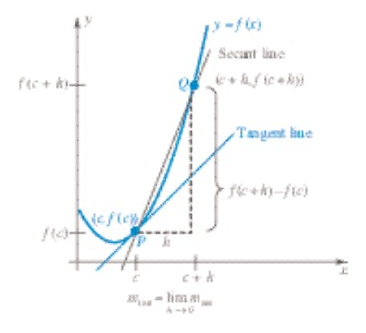
Gambar 1. Ilustrasi garis singgung pada suatu kurva
Dari Gambar 1 di atas, apabila \(h\) cukup kecil maka titik \(Q\) akan mendekati titik \(P\). Untuk \(h\) mendekati nol maka arah talibusur \(PQ\) (\(m_{sec}\)) menjadi gradien atau arah garis singgung (tangent line) di titik \(P\). Hal ini dinyatakan dengan
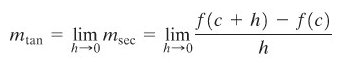
Dengan menggunakan konsep limit, yang mana telah kita pelajari pada bagian sebelumnya, sekarang kita bisa memberikan definisi yang formal untuk garis singgung.
DEFINISI:
Garis singgung kurva \(y=f(x)\) di titik \(P(c,f(c))\) adalah garis yang melalui titik \(P\) dengan kemiringan
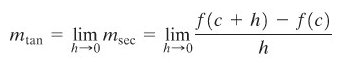
asalkan bahwa limit ini ada dan bukan \(∞\) atau \(-∞\).
Setelah kita memperoleh kemiringan garis singgung yang mana merupakan turunan dari fungsi tersebut, maka kita dapat mencari persamaan untuk garis singgungnya. Anda mungkin masih ingat bahwa persamaan garis singgung di titik \( P(x_1,y_1) \) pada kurva \(y = f(x)\) dengan gradien \(m\) ditentukan oleh rumus

CONTOH 1:
Cari kemiringan garis singgung pada kurva \(y=f(x)=x^2\) di titik (2, 4).
Pembahasan:
Pertama, kita akan mencari slope atau kemiringan garis singgung dengan menerapkan rumus definisi turunan. Kita peroleh

Garis yang kemiringannya (slope) kita cari diperlihatkan pada Gambar 2.

Gambar 2.
Contoh 2:
Carilah persamaan garis singgung untuk kurva \(y = 2/x\) di titik (2,1) pada kurva ini.
Pembahasan:
Pertama, kita akan mencari slope atau kemiringan garis singgung dengan menerapkan rumus definisi turunan dengan \(f(x) = 2/x\) dan \(x_0 = 2\). Kita peroleh

Dengan demikian, persamaan garis singgung di (2,1) adalah
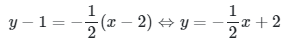
Persamaan garis singgung dan kurva \(y = 2/x\) dapat dilihat pada Gambar berikut.

Gambar 3.
Contoh 3:
Carilah persamaan garis singgung untuk kurva \(y = \sqrt{x} \) di \(x = 4\).
Pembahasan:
Pertama, kita akan mencari slope atau kemiringan garis singgung dengan mencari turunan untuk \(f(x) = \sqrt{x}\). Kita peroleh

Dengan demikian, persamaan garis singgung yang melalui titik (4,2) dengan kemiringan 1/4 adalah

Persamaan garis singgung dan kurva \(y = \sqrt{x}\) dapat dilihat pada Gambar berikut.

Gambar 4.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
To be successful, you must act big, think big and talk big.
