www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Lingkaran › Menentukan Persamaan Lingkaran
Menentukan Persamaan Lingkaran
Lingkaran dapat dibuat dengan titik pusat O(0,0) atau titik pusat pada koordinat-koordinat lainnya, yaitu M(a,b). Lingkaran dengan titik pusat O(0,0) dan M(a,b) mempunyai persamaan lingkaran yang berbeda.
Dalam kehidupan sehari-hari, tentu banyak Anda temui pemanfaatan bentuk lingkaran, misalnya ban sepeda. Sebuah lingkaran adalah himpunan titik-titik pada bidang yang berjarak sama terhadap sebuah titik tetap. Titik tetap itu disebut pusat lingkaran dan jarak titik tetap itu ke titik tertentu disebut jari-jari lingkaran.
Lingkaran dapat dibuat pada bidang Cartesius, yang terdiri dari sumbu x dan sumbu y. Lingkaran dapat dibuat dengan titik pusat O(0,0) atau titik pusat pada koordinat-koordinat lainnya, yaitu M(a,b). Lingkaran dengan titik pusat O(0,0) dan M(a,b) mempunyai persamaan lingkaran yang berbeda.
Persamaan Lingkaran Berpusat di O(0,0) dan Jari-jari r.
Perhatikan Gambar 1 di mana lingkaran berpusat pada O(0,0) dan mempunyai jari-jari r. Misalkan P(x,y) terletak pada lingkaran. Menurut definisi:
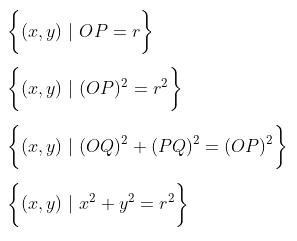

Gambar 1. Lingkaran berpusat di O(0,0) dan jari-jari r
Jadi, persamaan lingkaran yang berpusat di O(0,0) dan mempunyai jari-jari r adalah

Perhatikan contoh soal berikut:
Contoh 1:
Tentukanlah persamaan lingkaran yang berpusat di O(0,0) dan (i) berjari-jari 4; (ii) melalui titik (3,-2).
Pembahasan:
Persamaan lingkaran pada (i) adalah \(x^2+y^2=16\) (r=4)
Pada (ii), persamaan lingkaran \(x^2+y^2=r^2\) melalui titik (3,-2) sehingga x = 3 dan y = -2. Untuk mencari persamaan lingkaran ini, kita perlu mencari nilai r terlebih dahulu, yaitu:

Jadi, persamaan lingkaran yang berpusat di O(0,0) dan melalui titik (3,-2) adalah \(x^2+y^2=13\).
Persamaan Lingkaran yang Berpusat di M(a,b) dan Jari-jari r.
Amati Gambar 2 di mana Lingkaran berpusat pada M(a,b) dan mempunyai jari-jari r. Misalkan P(x,y) terletak pada lingkaran.
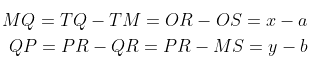

Gambar 2. Lingkaran berpusat di M(a,b) dan jari-jari r
Menurut definisi:
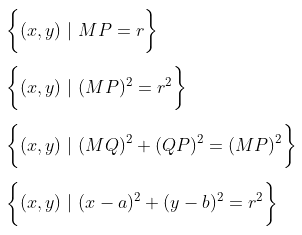
Jadi, persamaan garis lingkaran yang berpusat di M(a,b) dan jari-jari r adalah

Perhatikan contoh soal berikut:
Contoh 2:
Tentukanlah persamaan lingkaran yang berpusat di (4,-3) dan (i) berjari-jari 5; (ii) melalui titik (2,1).
Pembahasan:
Persamaan lingkaran pada (i) adalah

Persamaan lingkaran pada (ii) melalui titik (2,1) sehingga \(x = 2\) dan \(y = 1\). Untuk mencari persamaan lingkaran ini, kita perlu mencari nilai r terlebih dahulu yakni

Jadi, persamaan lingkaran yang berpusat di (4,-3) dan melalui titik (2,1) adalah
\[ (x-4)^2+(y+3)^2=20 \]
Persamaan Umum Lingkaran
Lingkaran mempunyai persamaan umum, yaitu:

Titik pusatnya adalah (-A, -B) dan jari-jarinya adalah r yakni

Bukti:
Jika bentuk umum persamaan lingkaran yang digunakan adalah \[ x^2+y^2+Ax+By+C=0 \] maka pusat lingkarannya adalah

dan jari-jarinya adalah

Perhatikan contoh soal berikut:
Contoh 3:
Tentukanlah titik pusat dan jari-jari lingkaran yang mempunyai persamaan:

Pembahasan:
Persamaan lingkaran \(x^2+y^2-4x+6y-12=0\) merupakan bentuk umum persamaan lingkaran, yaitu \(x^2+y^2+2Ax+2By+C=0\). Dengan membandingkan letak nilai yang bersesuaian diperoleh:
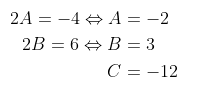
Sehingga pusat lingkaran (-A,-B) = (2,-3) dan jari-jari lingkaran (r) adalah

Jadi, titik pusat dan jari-jari lingkaran yang mempunyai persamaan: \(x^2+y^2-4x+6y-12=0\) adalah (2,-3) dan 5.
Contoh 4:
Tentukan persamaan lingkaran yang melalui titik (3,2), (-1,6) dan (-1,2).

Gambar 3. Lingkaran yang melalui titik (3,2), (-1,6) dan (-1,2).
Pembahasan:
Misalkan persamaan lingkaran:

Jika melalui titik (3,2), maka

Jika melalui titik (-1,6), maka

Jika melalui titik (-1,2) maka

Dari persamaan (1) dan (2), diperoleh

Dari persamaan (2) dan (3), diperoleh

Substitusi persamaan (5) ke persamaan (4), diperoleh
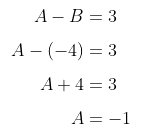
Nilai A dan B yang diperoleh dari perhitungan di atas disubstitusi ke persamaan (1) sehingga diperoleh:
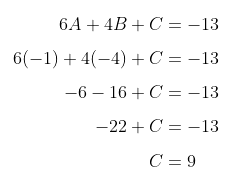
Dengan demikian, persamaan lingkarannya adalah:

Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
To know another is not to know the person's face, but to know the person's heart.
