www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Pertidaksamaan › Pertidaksamaan Matematika: Rumus, contoh soal dan pembahasan
Pertidaksamaan Matematika: Rumus, contoh soal dan pembahasan
Salah satu masalah utama dari pertidaksamaan yaitu mencari solusi penyelesaian yang memenuhi pertidaksamaan tersebut. Solusi tersebut bisa berupa suatu titik, interval, atau himpunan.
Dalam matematika ada sebuah konsep yang namanya pertidaksamaan. Bentuk baku pertidaksamaan dalam notasi matematika dapat dituliskan dengan \(P(x)≥0\), di mana \(P(x)\) merupakan suatu polinomial (tanda \(≥\) bisa juga digantikan dengan \(≤,<\), atau \(>\)).
Contoh pertidaksamaan misalnya,

Perhatikan bahwa pertidaksamaan pertama disebut pertidaksamaan linear, pertidaksamaan kedua merupakan contoh pertidaksamaan kuadrat, dan pertidaksamaan ketiga merupakan pertidaksamaan pecahan atau hasil bagi.
Salah satu masalah utama dari pertidaksamaan adalah mencari solusi atau himpunan penyelesaian yang memenuhi pertidaksamaan tersebut. Himpunan penyelesaian suatu pertidaksamaan adalah himpunan bilangan yang mana menyebabkan pertidaksamaan tersebut bernilai benar. Solusi tersebut bisa berupa suatu titik, interval, atau himpunan.
Sebagai contoh sederhana, solusi pertidaksamaan untuk \(x-2 < 0 \) adalah semua nilai \(x\) yang menyebabkan pertidaksamaan tersebut bernilai benar yakni ketika nilai \(x\) tersebut dikurangi dengan 2 akan menghasilkan nilai kurang dari nol. Nilai \(x\) yang memenuhi tersebut adalah himpunan bilangan yang kurang dari 2 atau kita nyatakan dengan \(x < 2\) (misalnya \(x = -100, \ x = -3, \ x = 1\) atau nilai \(x\) lainnya yang kurang dari 2.
Dalam contoh ini solusi pertidaksamaan adalah berupa suatu interval atau himpunan. Anda bisa temukan lebih banyak contoh lain di bawah ini, tetapi terlebih dahulu saya akan jelaskan sedikit mengenai selang atau interval bilangan karena ini sangat penting dalam materi pertidaksamaan.
Selang atau Interval bilangan
Menyelesaikan suatu pertidaksamaan (misalnya, \(3x-6 < 12)\) berbeda dengan menyelesaikan suatu persamaan (misalnya, \(3x-6=12 \)). Dalam persamaan, himpunan penyelesaian biasanya terdiri dari satu bilangan atau mungkin sejumlah bilangan berhingga, sedangkan himpunan penyelesaian suatu pertidaksamaan biasanya terdiri dari suatu selang atau interval bilangan.
Oleh karena itu, di sini akan diperkenalkan terlebih dahulu beberapa jenis selang dan cara penulisannya yang akan sering muncul dalam pembahasan selanjutnya.
Interval \(a < x < b\) menunjukkan selang terbuka yang terdiri dari semua bilangan antara \(a\) dan \(b\), tidak termasuk titik-titik ujung \(a\) dan \(b\). Kita nyatakan dengan lambang \((a,b)\) (Gambar 1). Sebaliknya, interval \(a ≤ x ≤ b\) menunjukkan selang tertutup, yang mencakup titik-titik ujung \(a\) dan \(b\) yang mana dinyatakan dengan \([a,b]\) (Lihat Gambar 2).
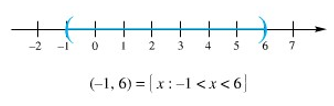
Gambar 1. Selang \(a < x < b \ \) untuk \(a = -1\) dan \(b = 6\)

Gambar 2. Selang \(a ≤ x ≤ b \ \) untuk \(a = -1\) dan \(b = 5\)
Tabel 1 berikut ini menunjukkan sejumlah kemungkinan dari jenis selang dan cara penulisannya.
Tabel 1. Berbagai kemungkinan jenis selang dan cara penulisannya

Operasi Pertidaksamaan
Prosedur untuk menyelesaikan suatu pertidaksamaan mirip dengan prosedur menyelesaikan suatu persamaan. Berikut adalah operasi-operasi tertentu yang bisa dilakukan untuk menyelesaikan suatu pertidaksamaan:
- Kita dapat menambahkan bilangan yang sama pada kedua ruas suatu pertidaksamaan;
- Kita dapat mengalikan kedua ruas suatu pertidaksamaan dengan suatu bilangan positif;
- Kita dapat mengalikan kedua ruas dengan suatu bilangan negatif, tetapi kemudian kita harus membalikkan arah tanda pertidaksamaan. Operasi ketiga inilah yang membedakan penyelesaian suatu pertidaksamaan dengan suatu persamaan.
Sifat-sifat Pertidaksamaan
Sebelum kita membahas lebih banyak contoh mengenai pertidaksamaan, terlebih dahulu pahamilah sifat-sifat pertidaksamaan berikut ini:
- Jika \(a < b\) maka \(a + c < b + c\)
- Jika \(a < b\) dan \(c < d\) maka \(a + c < b + d\)
- Jika \(a < b\) dan \(c > 0\) maka \(ac < bc\)
- Jika \(a < b\) dan \(c < 0 \) maka \(ac > bc\)
- Jika \(0 < a < b\) maka \(\frac{1}{b} < \frac{1}{a}\)
Jenis-jenis Pertidaksamaan
Ada banyak bentuk pertidaksamaan matematika, beberapa di antaranya, yaitu:
- Pertidaksamaan linear
- Pertidaksamaan kuadrat
- Pertidaksamaan pecahan atau hasil bagi
- Pertidaksamaan irasional (bentuk akar)
- Pertidaksamaan mutlak
- Pertidaksamaan eksponen
- Pertidaksamaan logaritma
- Pertidaksamaan pangkat tinggi
Contoh soal pertidaksamaan linear
Berikut dua contoh terkait pertidaksamaan linear. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan linear
Contoh 1:
Selesaikanlah pertidaksamaan \(2x-7 < 4x-2\) dan perlihatkan grafik himpunan penyelesaiannya.
Pembahasan:
Pertama kita menambahkan kedua ruas dengan 7 dan kemudian menambahkan \(-4x\). Setelah itu, kalikan dengan -1/2. Kita peroleh berikut:

Grafik himpunan penyelesaiannya tampak dalam Gambar 3 berikut:

Gambar 3. Himpunan penyelesaian \(2x-7 < 4x-2\)
Contoh 2:
Selesaikan pertidaksamaan \(-5≤2x+6≤4\).
Pembahasan:
Pertama kita menambahkan -6 dan kemudian mengalikan dengan 1/2 pada pertidaksamaan tersebut sehingga diperoleh:

Gambar 4 berikut memperlihatkan grafik himpunan penyelesaiannya.

Gambar 4. Himpunan penyelesaian \(-5≤2x+6≤4\)
Contoh soal pertidaksamaan kuadrat
Berikut dua contoh terkait pertidaksamaan kuadrat. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan kuadrat
Contoh 3:
Himpunan penyelesaian dari pertidaksamaan kuadrat \( x^2-8x+15 \leq 0 \) untuk \(x \in R\) adalah…
- \( \{ x | -5 \leq x \leq -3 \} \)
- \( \{ x | 3 \leq x \leq 5 \} \)
- \( \{ x | x \leq -5 \ \text{atau} \ x \geq -3 \} \)
- \( \{ x | x \leq -3 \ \text{atau} \ x \geq 5 \} \)
- \( \{ x | x \leq -3 \ \text{atau} \ x \geq -5 \} \)
Untuk menyelesaikan soal ini kita bisa faktorkan pertidaksamaan kuadrat di atas. Perhatikan berikut ini:
Selanjutnya, dari hasil di atas kita buat garis bilangannya seperti pada gambar di bawah.

Karena notasi pertidaksamaan kurang dari sama dengan \( (\leq) \), maka himpunan penyelesaiannya ditunjukkan oleh garis bilangan bertanda negatif atau pada interval \( 3 \leq x \leq 5 \).
Jawaban B.
Contoh 4:
Himpunan penyelesaian dari pertidaksamaan kuadrat \(x^2-5x-6 > 0\) untuk \(x \in R\) adalah…
- \( \{ x | x < -1 \ \text{atau} \ x > 6 \} \)
- \( \{ x | x < 2 \ \text{atau} \ x > 3 \} \)
- \( \{ x | -3 < x < 2 \} \)
- \( \{ x | x < -6 \ \text{atau} \ x > 6 \} \)
- \( \{ x | -6 < x < 1 \} \)
Untuk menyelesaikan soal ini, kita bisa faktorkan bentuk pertidaksamaan kuadratnya, yakni:
Selanjutnya, dari hasil di atas kita bisa buat garis bilangannya seperti pada gambar di bawah.

Karena notasi pertidaksamaan pada soal di atas adalah lebih dari (>), maka himpunan penyelesaian ditunjukkan oleh garis bilangan dengan tanda positif atau pada interval \( \{ x|x < -1 \ \text{atau} \ x > 6 \} \).
Jawaban A.
Contoh soal pertidaksamaan pecahan (hasil bagi)
Berikut dua contoh terkait pertidaksamaan pecahan. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan pecahan
Contoh 5: SBMPTN 2015
Himpunan penyelesaian pertidaksamaan \( \frac{12}{x+1} < \frac{x}{6} \) adalah…
- \( \{ x \in R | -1 < x < 8 \} \)
- \( \{ x \in R | -9 < x < -1 \ \text{atau} \ x > 8 \} \)
- \( \{ x \in R | x < -9 \ \text{atau} \ 1 < x < 8 \} \)
- \( \{ x \in R | x \leq -1 \ \text{atau} \ 8 < x < 9 \} \)
- \( \{ x \in R | x < -9 \ \text{atau} \ -1 < x < 8 \} \)
Lakukan operasi aljabar untuk membuat ruas kanan pertidaksamaan menjadi nol:
Syarat pertama dari pertidaksamaan di atas adalah \( x + 1 \neq 0 \) maka \( x \neq -1 \).
Berikutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:
- Pembuat nol pembilang: \( (x+9)(x-8) = 0 \) maka \( x = -9 \) atau \(x = 8\)
- Pembuat nol penyebut: \( x+1 = 0 \) maka \( x = -1\).
Gambarkan nilai-nilai \(x\) pembuat nol pada garis bilangan dan lakukan uji titik \(x\) pada tiap-tiap interval bilangan. Kita peroleh berikut:

Dari gambar kita bisa ambil kesimpulan bahwa daerah \( -9\leq x \leq -1 \) atau \( x \geq 8 \) merupakan himpunan penyelesaian soal karena pada daerah ini \( \frac{(x+9)(x-8)}{6(x+1)} > 0 \).
Lalu dengan memperhatikan syarat pertama yaitu \( x \neq -1 \) maka himpunan penyelesaian yang memenuhi adalah \( -9 < x < -1 \) dan \( x > 8 \).
Jawaban B.
Contoh 6: SBMPTN 2016
Semua nilai \(x\) yang memenuhi \( \frac{3}{x}-\frac{3}{x+3} \leq 0 \) adalah…
- \( x < 0 \)
- \( -3 \leq x \leq 0 \)
- \( -3 < x < 0 \)
- \( x < -3 \) atau \( x > 0 \)
- \( x \leq -3 \) atau \( x \geq 0 \)
Lakukan operasi aljabar untuk menyederhanakan pertidaksamaan menjadi bentuk umum pertidaksamaan pecahan, yaitu:
Syarat pertama dari pertidaksamaan di atas adalah \( x(x+3) \neq 0 \) sehingga \(x = 0\) atau \(x = -3\).
Berikutnya kita cari batas atau pembuat nol pada pembilang dan penyebut, yaitu:
- Pembuat nol pembilang: tidak ada
- Pembuat nol penyebut adalah \( x(x+3)=0 \) maka \( x = 0 \) atau \(x = -3\).
Gambarkan nilai-nilai \(x\) pembuat nol pada garis bilangan dan lakukan uji titik \(x\) pada tiap-tiap interval bilangan. Kita peroleh berikut:
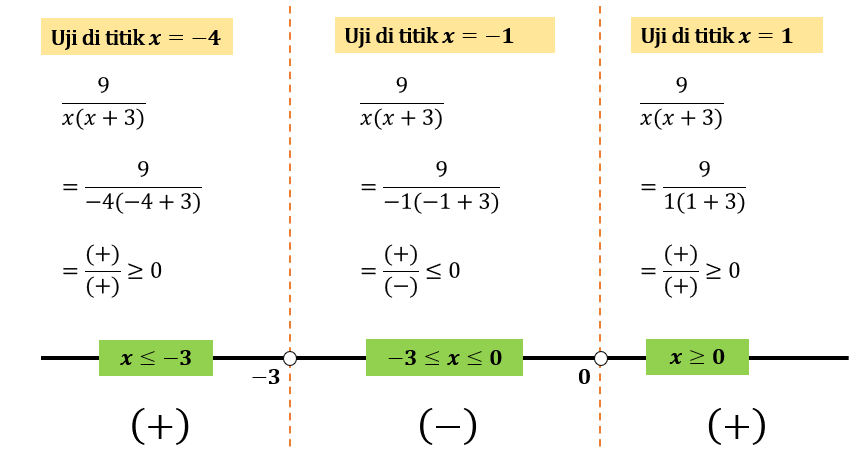
Dari gambar bisa diambil kesimpulan bahwa daerah \( -3 \leq x \leq 0 \) merupakan himpunan penyelesaian soal karena pada daerah ini \( \frac{9}{x(x+3)} \leq 0 \).
Lalu dengan memperhatikan syarat pertama yaitu \( x \neq 0 \) atau \( x \neq -3 \) maka himpunan penyelesaian yang memenuhi adalah \( -3 < x < 0 \).
Jawaban C.
Contoh soal pertidaksamaan irasional (bentuk akar)
Berikut dua contoh terkait pertidaksamaan bentuk akar. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan bentuk akar
Contoh 7: SBMPTN 2018
Himpunan penyelesaian \( x - \sqrt{6-x} \geq 0 \) adalah…
- \( \{ x | x < -3 \ \text{atau} \ x \geq 2 \} \)
- \( \{ x | x \leq -3 \ \text{atau} \ 2 \leq x \leq 6 \} \)
- \( \{ x | 0 \leq x \leq 6 \} \)
- \( \{ x | 2 \leq x \leq 6 \} \)
- \( \{ x | x \leq 6 \} \)
Untuk menyelesaikan pertidaksamaan bentuk akar di atas, ada beberapa tahapan yang perlu diperiksa.
Pertama, kita coba selesaikan pertidaksamaan dengan menyamakan bentuk kiri dan kanan, bisa dengan mengkuadratkan ruas kiri dan kanan pertidaksamaan tersebut. Berikut hasil yang diperoleh:

Dari hasil di atas diperoleh himpunan penyelesaian pertidaksamaan kuadrat di atas adalah \( x \leq -3 \) atau \(x \geq 2\).
Kedua, tentukan nilai \(x\) agar bentuk akar \( \sqrt{6-x} \) terdefinisi atau mempunyai nilai real. Agar \( \sqrt{6-x} \) mempunyai nilai real, maka syaratnya yaitu:
Ketiga, karena \( 6-x \geq 0 \) dan agar \( x - \sqrt{6-x} \geq 0 \) mempunyai nilai real, maka \(x \geq 0\).
Dari ketiga tahapan penyelesaian di atas, irisan dari ketiga nilai \(x\) yang diperoleh adalah himpunan penyelesaian pertidaksamaan akar yang diberikan dalam soal. Jika digambarkan hasilnya kurang lebih seperti berikut:

Dari hasil di atas, himpunan penyelesaiannya adalah \( HP: \{ x | 2 \leq x \leq 6 \} \).
Jawaban D.
Contoh 8: SIMAK UI 2018
Himpunan penyelesaian dari pertidaksamaan \( \sqrt{x^2-4} \leq 3-x \) adalah…
- \( \left\{ x \in R: x \leq -2 \ \text{atau} \ 2 \leq x \leq \frac{13}{6} \right\} \)
- \( \left\{ x \in R: x \leq -2 \ \text{atau} \ 2 \leq x \right\} \)
- \( \left\{ x \in R: -2 \leq x \leq \frac{13}{6} \right\} \)
- \( \left\{ x \in R: x \leq \frac{13}{6} \right\} \)
- \( \left\{ x \in R: 2 \leq x \leq \frac{13}{6} \right\} \)
Untuk menyelesaikan pertidaksamaan bentuk akar di atas, ada beberapa tahapan yang perlu diperiksa.
Pertama, kita coba selesaikan pertidaksamaan dengan mengkuadratkan ruas kiri dan kanan pertidaksamaan tersebut. Berikut hasil yang diperoleh:

Dari hasil di atas diperoleh himpunan penyelesaian \( x \leq \frac{13}{6} \).
Kedua, tentukan nilai \(x\) agar bentuk akar \( \sqrt{x^2-4} \) terdefinisi atau mempunyai nilai real. Agar \( \sqrt{x^2-4} \) mempunyai nilai real, maka syaratnya yaitu:

Ketiga, karena \( \sqrt{x^2-4} \geq 0 \) dan agar \( \sqrt{x^2-4} \leq 3-x \) mempunyai nilai real, maka:
Dari ketiga tahapan penyelesaian di atas, irisan dari ketiga nilai \(x\) yang diperoleh adalah himpunan penyelesaian pertidaksamaan akar yang diberikan dalam soal. Jika digambarkan hasilnya kurang lebih seperti berikut:

Dari hasil di atas, himpunan penyelesaiannya adalah \( HP: \left\{ x \in R : x \leq -2 \ \text{atau} \ 2 \leq x \leq \frac{13}{6} \right\} \).
Jawaban A.
Contoh soal pertidaksamaan mutlak
Berikut dua contoh terkait pertidaksamaan mutlak. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan mutlak
Contoh 9:
Himpunan penyelesaian dari \( |2x+5| \leq 6 \) adalah…
- \( \{ x| -\frac{11}{2} \leq x \leq \frac{1}{2} \} \)
- \( \{ x| -\frac{11}{2} \leq x \leq -\frac{1}{2} \} \)
- \( \{ x| \frac{1}{2} \leq x \leq \frac{11}{2} \} \)
- \( \{ x| -\frac{11}{2} \leq x \leq \frac{11}{2} \} \)
- \( \{ x| x \leq -\frac{11}{2} \ \text{atau} \ x \geq \frac{11}{2} \} \)
Dengan menggunakan sifat pertidaksamaan nilai mutlak, diperoleh berikut:
Jadi, himpunan penyelesaian dari pertidaksamaan \( |2x+5| \leq 6 \) adalah \( \{ -\frac{11}{2} \leq x \leq \frac{1}{2} \} \).
Jawaban A.
Contoh 10: SBMPTN 2017
Jika himpunan penyelesaian \( |2x-a| < 5 \) adalah \( \{ x | -1 < x < 4 \} \), maka nilai \(a\) adalah…
- \( -4 \)
- \( -3 \)
- \( -1 \)
- \( 3 \)
- \( 4 \)
Ingat sifat pertidaksamaan nilai mutlak, yaitu:
- Untuk \( |f(x)| < a \) maka himpunan penyelesaiannya adalah \( \{ x | -a < f(x) < a \} \)
- Untuk \( |f(x)| > a \) maka himpunan penyelesaiannya adalah \( \{ x | f(x) < -a \ \text{atau} \ f(x) > a \} \).
Berdasarkan sifat pertidaksamaan nilai mutlak di atas, maka himpunan penyelesaian pertidaksamaan \( |2x-a| < 5 \), yaitu:
Himpunan penyelesaian di atas ekuivalen dengan \( \{ x | -1 < x < 4 \} \) sehingga dapat disimpulkan:
Jadi, nilai \(a\) sama dengan 3.
Jawaban D.
Contoh soal pertidaksamaan eksponen
Berikut dua contoh terkait pertidaksamaan eksponen. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan eksponen
Contoh 11: SBMPTN 2019
Nilai \(x\) bilangan real yang memenuhi pertidaksamaan \( \frac{8}{a^x + 2} > a^x \) dengan \(a > 1\) adalah…
- \( x < \ ^a \! \log a \)
- \( x < \ ^a \! \log 2 \)
- \( x > \ ^{-2} \! \log a \)
- \( x > \ ^2 \! \log a \)
- \( x > \ ^a \! \log 2 \)
Untuk menyederhanakan penulisan pertidaksamaan, kita misalkan \( a^x = m \) di mana \( m > 0\) sehingga diperoleh:
Selanjutnya, karena di awal kita misalkan \( m = a^x\), maka \( -4 < a^x < 2 \) sehingga diperoleh berikut:
Himpunan penyelesaian dari pertidaksamaan \( \frac{8}{a^x + 2} > a^x \) dengan \(a > 1\) adalah irisan dari \(x < \ ^a \! \log 2 \) dan \( x \in R\) yaitu \( x < \ ^a \! \log 2 \).
Jawaban B.
Contoh 12: SBMPTN 2019
Jika \( 0 < a < 1\) maka \( \frac{ a^x + 2}{a^x} < a^x \) mempunyai penyelesaian…
- \( x < \ ^a \! \log 2 \)
- \( x < - \ ^a \! \log 2 \)
- \( x > \ ^a \! \log 2 \)
- \( x > - \ ^a \! \log 2 \)
- \( x < \ ^a \! \log 4 \)
Untuk menyederhanakan penulisan pertidaksamaan, kita misalkan \( a^x = m \) di mana \( m > 0\) sehingga diperoleh:
Selanjutnya, karena di awal kita misalkan \( m = a^x\), maka \( a^x < -1 \) atau \( a^x > 2 \) sehingga diperoleh berikut:
- Untuk \( a^x < -1 \) dan \( 0 < a < 1\) maka tidak ada nilai \(x\) yang memenuhi.
- Untuk \( a^x > 2\) dan \(0 < a < 1\), maka berlaku:
Jadi, himpunan penyelesaian pertidaksamaan \( \frac{ a^x + 2}{a^x} < a^x \) dengan \( 0 < a < 1\) adalah \(x < \ ^a \! \log 2\).
Jawaban C.
Contoh soal pertidaksamaan logaritma
Berikut dua contoh terkait pertidaksamaan logaritma. Untuk materi dan contoh soal lainnya, kunjungi link berikut: Contoh soal dan pembahasan pertidaksamaan logaritma
Contoh 13: UTBK-SBMPTN 2019
Himpunan penyelesaian dari pertidaksamaan \( (\log_a x)^2 + 4 \log_a x + 3 < 0 \) dengan \(a > 1\) adalah…
- \( a^{-3} < x < a^{-1} \)
- \( a^{-1} < x < a^{3} \)
- \( a^{-1} < x < a^{-3} \)
- \( a^{-3} < x < a \)
- \( 1 < x < a^{-3} \} \)
Sebelum kita jawab soal ini, ingat bahwa jika \( {}^a \! \log f(x) > {}^a \! \log g(x) \), maka untuk \( a > 1 \) berlaku \( f(x) > g(x) \) dan untuk \( 0 < a < 1 \) berlaku \( f(x) < g(x) \).
Untuk menyelesaikan soal ini kita bisa sederhanakan pertidaksamaan logaritma di atas dengan memisalkan \( \log_a x = m \). Kita peroleh berikut ini:
Dari hasil di atas, kita peroleh himpunan penyelesaian pertidaksamaannya yaitu \( -3 < m < -1 \).
Selanjutnya, kita kembalikan nilai \( m = \log_a x \). Perhatikan berikut ini:
Jadi, himpunan penyelesaian (HP) dari pertidaksamaan logaritma di atas adalah \( a^{-3} < x < a^{-1} \).
Jawaban A.
Contoh 14: UTBK-SBMPTN 2019
Himpunan penyelesaian dari pertidaksamaan \( (\log_a x)^2 - \log_a x -2 > 0 \) dengan \( 0 < a < 1 \) adalah…
- \( x < a^2 \ \text{atau} \ x > a^{-1} \)
- \( x < a^2 \ \text{atau} \ x > a^{-2} \)
- \( a^{2} < x < a^{-1} \)
- \( a^{2} < x < a^{-2} \)
- \( a^{-2} < x < a^{2} \} \)
Sebelum kita jawab soal ini, ingat bahwa jika \( {}^a \! \log f(x) > {}^a \! \log g(x) \), maka untuk \( a > 1 \) berlaku \( f(x) > g(x) \) dan untuk \( 0 < a < 1 \) berlaku \( f(x) < g(x) \).
Untuk menyelesaikan pertidaksamaan logaritma di atas, kita bisa misalkan \( \log_a x = m \) sehingga kita peroleh berikut:
Dari hasil di atas kita peroleh himpunan penyelesaian pertidaksamaan kuadratnya yaitu \(m < -1\) atau \(m>2\).
Selanjutnya, kita kembalikan nilai \( m = \log_a x \). Perhatikan berikut ini:
Jadi, himpunan penyelesaian (HP) dari pertidaksamaan logaritma di atas yaitu \( x < a^2 \) atau \(x > a^{-1} \).
Jawaban A.
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The greatest danger for most of us is not that our aim is too high and we miss it, but that it is too low and we reach it.
