Matematika Dasar   »   Fungsi   ›  Perbedaan antara Relasi dan Fungsi

Relasi & Fungsi

Perbedaan antara Relasi dan Fungsi

Relasi dapat diartikan sebagai hubungan antara daerah asal (domain) dan daerah kawan (kodomain). Sedangkan fungsi adalah relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya.

Secara sederhana, relasi dapat diartikan sebagai hubungan antara daerah asal (domain) dan daerah kawan (kodomain). Sedangkan fungsi adalah relasi yang memetakan atau memasangkan setiap anggota himpunan daerah asal (domain) tepat satu ke himpunan daerah kawannya (kodomain). Dengan kata lain, perbedaan antara relasi dan fungsi terletak pada cara memasangkan anggota himpunan daerah asal dengan daerah kawannya.

Dalam relasi, setiap anggota himpunan daerah boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal mempunyai pasangan dan dipasangkan hanya tepat satu dengan daerah kawannya. Untuk lebih jelasnya, perhatikan ilustrasi antara relasi dan fungsi berikut ini.

Perhatikan kembali ilustrasi di atas. Anggota himpunan dalam daerah A disebut daerah asal atau domain dan anggota himpunan dalam daerah B disebut daerah kawan atau kodomain. Dua gambar yang pertama menunjukkan relasi dan bukan fungsi karena setiap anggota himpunan daerah asal ada yang tidak mempunyai pasangan atau mempunyai pasangan lebih dari satu pada daerah kawannya.

Sementara itu, gambar yang ketiga dari ilustrasi di atas menunjukkan kasus khusus dari relasi yang disebut fungsi karena setiap anggota himpunan dari daerah asal dipasangkan tepat satu pada daerah kawannya.

Jenis-jenis Fungsi

Secara umum, fungsi dapat dikelompokkan menjadi tiga jenis yakni fungsi injektif, fungsi surjektif dan fungsi bijektif. Kita akan membahas satu demi satu fungsi tersebut berikut ini.

#1. Fungsi injektif

Fungsi injektif disebut juga fungsi satu-satu. Fungsi \( f: A \to B \) dikatakan fungsi injektif jika dan hanya jika anggota kodomain dipasangkan satu kali dengan anggota domain. Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, tapi semua anggota kodomain yang terpasangkan hanya ada satu, tidak boleh ada yang lebih dari satu. Perhatikan gambar berikut.

#2. Fungsi surjektif

Fungsi surjektif yaitu fungsi yang memiliki ciri bahwa anggota kodomainnya boleh memiliki pasangan lebih dari satu, tapi tidak boleh ada anggota kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi apabila jumlah anggota kodomain sama atau lebih banyak dari anggota domain. Untuk lebih jelasnya, perhatikan gambar berikut.

#3. Fungsi bijektif

Fungsi bijektif merupakan gabungan dari fungsi injektif dan fungsi surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat satu. Kebalikan fungsi dari fungsi injektif dan surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga merupakan fungsi/pemetaan. Perhatikan gambar di bawah. Perhatikan gambar berikut.

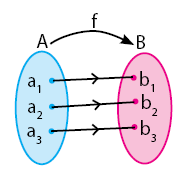
Terlihat bahwa kebalikan dari fungsi f juga merupakan fungsi atau pemetaan, bukan?

Sumber:

https://idschool.net/sma/relasi-dan-fungsi-pengertian-perbedaan-dan-contoh-soal/

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.